One major difference between immersion quenching and gas quenching is the presence of boiling during the early stages of quenching in oil or water. The formation of a vapor phase has a significant effect on the overall and local heat removal rate from the parts being quenched and also on part distortion. With the absence of a quenchant phase change, gas quenching is reported to result in more uniform heat extraction, thus lessening part distortion. However, gas quenching is not without inherent problems. Non-uniform gas flow around a part contributes to non-uniform cooling at different locations, and this in turn contributes to distortion. In particular, a thin walled ring gear was found to be prone to distortion due to difficulties in achieving uniform gas flow during quenching. Process variables investigated were fan speed and cooling durations for different quenching stages. The intent was to reduce distortion by controlling the overall gas velocity through adjustment of the fan speed, whereby the local cooling rates could be controlled to better accommodate the dimensional change associated with steel phase transformations during quenching.
Introduction
Vacuum carburization followed by gas quenching of steel parts has become more widely used by the heat treat industry over the past decade. Compared to the traditional gas carburization process, vacuum carburization reduces furnace time and generally provides improved control of the carbon profile in the case [Iwata, 2005]. Two main gases used as carbon sources are acetylene and propane. The tremendous effects of carbon in iron on hardness, strength, and hardenability are well known; the carbon content strengthens iron and changes the kinetics of austenite decomposition. For example, higher carbon content increases the incubation time for the start of bainite formation, while also decreasing the bainite formation rate. Higher carbon content also depresses the martensite phase transformation starting temperature. The effect of carbon content on phase transformations directly affects the internal stress condition during a quenching process. Because the vacuum carburization process provides flexibility in control of the carbon profile in the case, it is possible to optimize the vacuum carburization boost/diffuse schedule to improve the residual stress state in carburized and quench-hardened parts.
Most commercial gas quenching processes use high-pressure nitrogen as the quenching medium. Compared to traditional oil quenching, gas quenching is environmentally friendly and produces parts with clean surfaces, so washing after quenching is not required and quenchant disposal is a non-issue. Claims that gas quenching can provide more uniform cooling and less distortion than liquid quenching are generally accepted. However, care has to be given to the quenching chamber design, quenching process parameters, rack design, orientation of the parts, and the alloy hardenability. Quenching in chambers without reasonable gas flow uniformity can produce more distortion than liquid quenching. Gas quenching without enough cooling power to meet the commercial load demands can produce significant variance of distortion among parts at different locations in the rack, let alone not meet hardness requirements in all parts of the load.
Due to the combination of inherent thermal gradients and the material volume change associated with steel phase transformations, a certain level of dimensional change is inevitable in quench-hardened parts. However, distortion can be reduced to an acceptable level by improved control of carburization and quenching processes [Li & Grandhi, 2006]. The effects of gas flow and cooling rate on distortion of a vacuum carburized and gas quenched thin walled ring gear were investigated using a combination of numerical analysis and experimentally measured temperature histories at selected locations in the parts themselves and within the racked parts. DANTE, a finite element-based heat treatment simulation software, was used for the numerical analyses. Modelling results for several cooling practices and predicted changes in dimensions of the ring gear are presented.
Phase Transformation Kinetics
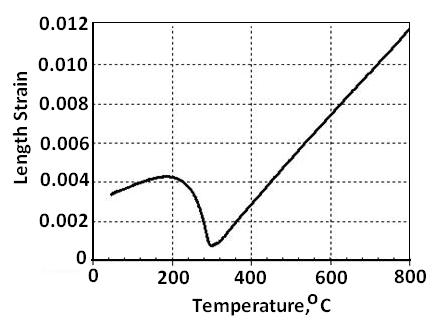
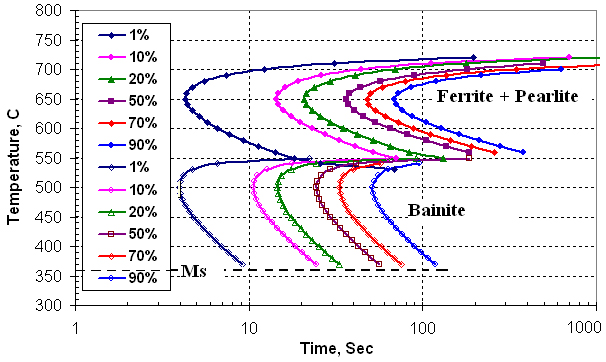
The ring gear was made of AISI 5130 steel with a nominal chemical composition of 0.83%Mn, 0.22%Si, 0.15%Ni, 0.80%Cr, 0.04%Mo, and 0.30%C (% indicates percentage by weight). The gear was carburized on all surfaces, so it is necessary to characterize the phase transformation kinetics over the range of carbon levels in the part in order to model the heat treatment process. In previous work, dilatometry experiments were conducted for the base carbon level and several intermediate levels up to 0.8% carbon for this steel grade [Ferguson & Dowling, 1997]. Figure 1(a) shows a dilatometry curve for a continuous cooling experiment for an AISI 5140 steel sample. The phase transformation kinetics parameters for both martensitic and diffusive phase transformations were determined from such dilatometry data and have been stored in the DANTE database. Isothermal and continuous cooling phase transformation diagrams, i.e. TTT and CCT curves, can be generated from these parameters, as shown by the TTT curve in Figure 1(b) for AISI 5130. These diagrams can be generated to assist in planning the heat treatment schedule for a given alloy and part geometry.
Ring Gear Geometry and Finite Element Model
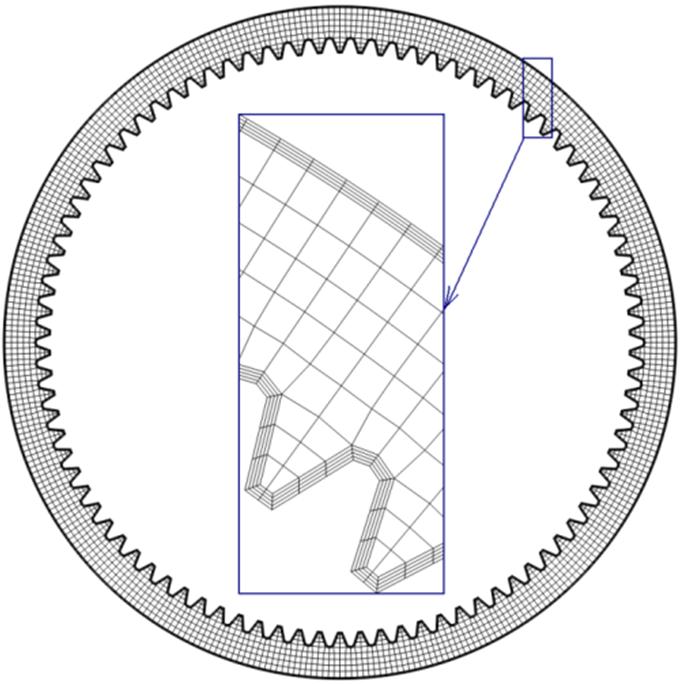
A solid model of the ring gear used in this study is shown in Figure 2(a). The outer diameter of the gear is 165mm, the inner (tip) diameter is 141mm, and the height is 20mm. There are a total number of 97 inner teeth, as shown. During the gas quenching process, thermal conduction through the thin wall (radial direction) is the dominant heat flow direction. Prone to distortion due to the thin wall, the main distortion mode is out-of-round distortion.
To effectively and efficiently predict the out-of-round distortion, a two-dimensional plane strain model was developed, as shown in Figure 2(b). The finite element model contains 8,010 nodes and 7,380 quadrilateral elements. To improve the calculation accuracy, fine surface elements are used where there are steep thermal, stress, and carbon gradients. Boundary conditions and material models were defined to simulate the vacuum carburization and high pressure nitrogen gas quenching process steps.
Vacuum Carburization
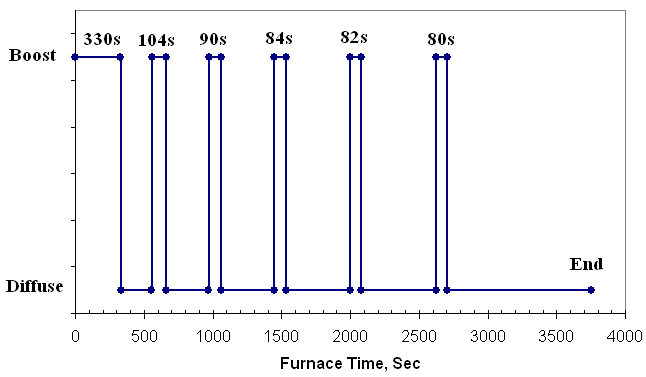
The required case depth for this gear was 0.5mm, with the case depth defined as the distance from the surface to a depth with carbon level of 0.4%. The aim surface carbon was 0.85%. For this gear, acetylene was used as carburizing gas. DANTE-VCARB, a finite element analysis tool, was used to determine a boost/diffuse schedule for the vacuum carburization process that would meet the surface carbon and case depth requirements. The vacuum carburization schedule determined is shown in Figure 3. The total boost time is 770 seconds and total furnace time is 3750 seconds, with the carburization temperature being 950 C.
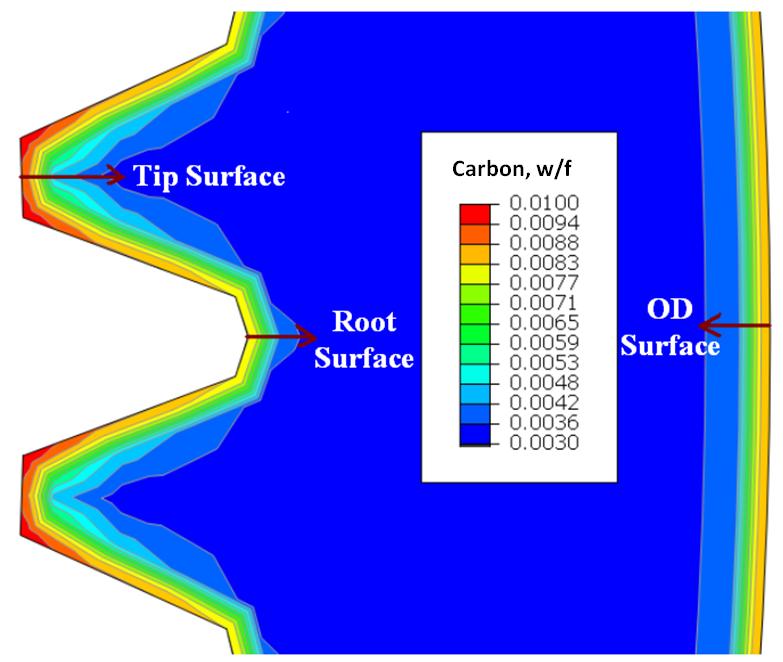
The predicted carbon distribution after carburization is shown in Figure 4(a). The carbon contents of the outer diameter surface, the gear root surface, and the gear tip surface have significant differences due to geometry, as shown in Figure 4(b).
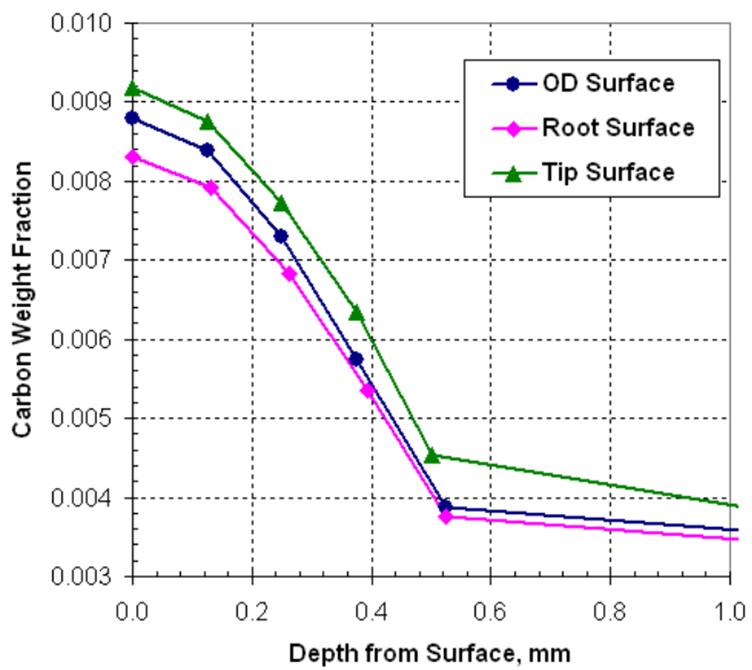
(b) Carbon distribution curve plots.
Modelling Distortion during Gas Quenching
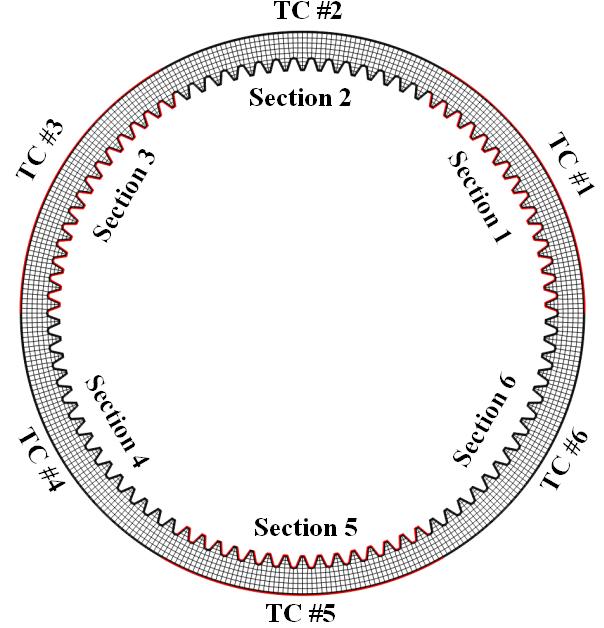
High pressure gas quenching of loaded racks of ring gears resulted in out-of-round distortion of many gears. The thought was that non-uniform cooling around the circumference of the gear was the cause of this distortion. Measured cooling histories of several gears at different locations in the rack showed that temperature non-uniformity was an issue. The particular gear discussed in this paper was instrumented with six thermocouples located in the gear at mid-height position, spaced every 60 degrees around the circumference. The temperature histories were supplied to DCT for reference. To model the cooling process, the surface of the gear was divided into six equal surface sections that were centered around the thermocouple locations as shown in Figure 5(a). Thermal boundary conditions were applied to each section, including both OD and ID surfaces.
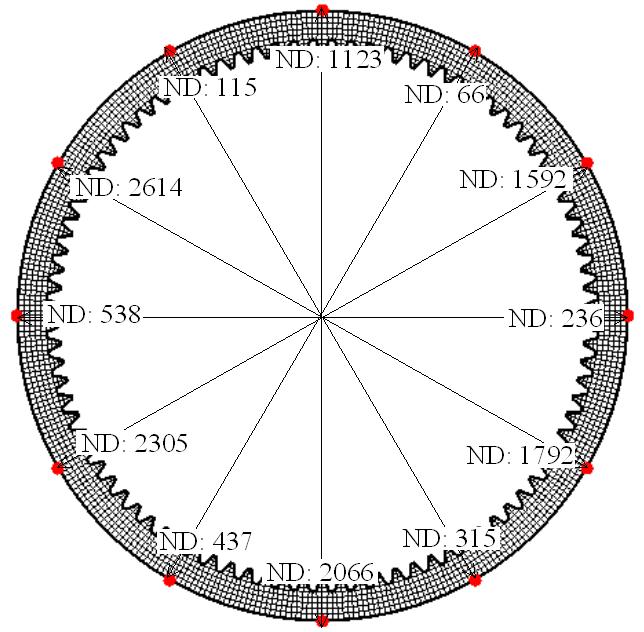
Six pairs of nodal points as shown in Figure 5(b) were used to calculate the out-of-round distortion. The intent was to document distortion caused by shape change and size change. Size change is consistent in general and can be compensated by adjusting the green geometry during gear design. Shape change is the undesirable distortion. After gas quenching, the distances between each pair of nodes were calculated, and the out-of-round distortion was defined as the difference between maximum and minimum distances.
The gears were carburized in a carburization chamber, and then transferred to a quenching chamber within 50 seconds. The temperature dropped about 50°C during this transfer period. Predicted cooling curves that coincided with three thermocouple (TC) locations when quenching this gear with 20 bar nitrogen at fan speeds of 40% and 100% of full speed are shown in Figure 6(a). The three locations were separated by 120 degrees of arc, and TC #1 and TC #5 had the fastest and slowest cooling rates among the six TCs. Heat transfer boundary conditions were determined, assuming the ring gear could be described by six uniformly sized circumferential sections. Figure 6(a) shows the predicted cooling curves for the three locations. Further details about the gear position and racking arrangement with other gears cannot be presented due to proprietary issues.
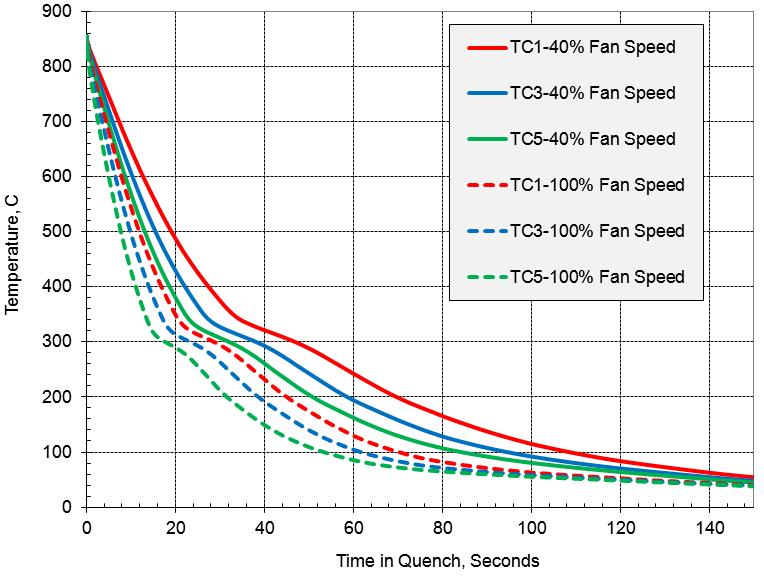
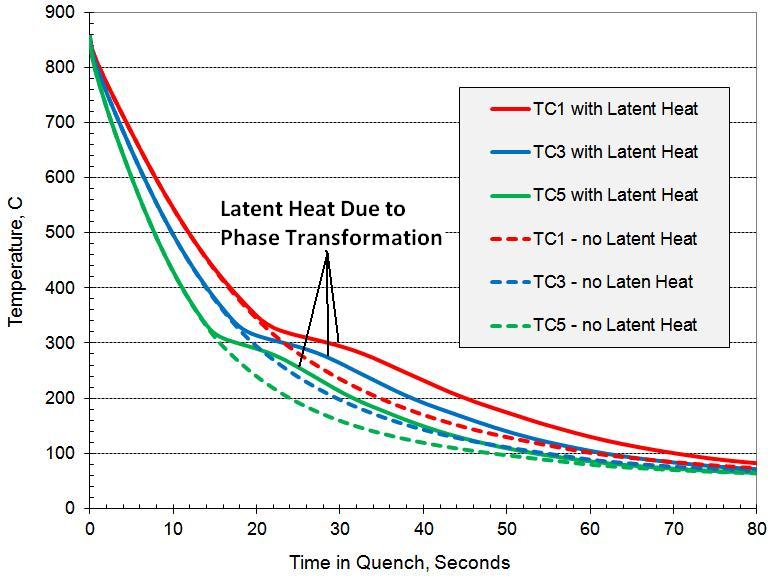
The latent heat effect for this gear geometry and steel grade was significant, and it was accounted for in the computer models. Figure 6(b) shows predicted cooling curves at 40% fan speed for models with and without latent heat evolution during the phase transformation. The additional energy due to latent heat released by the phase transformation at the TC locations is evident by the slope change in respective cooling curves. The predicted temperature difference caused by latent heat is more than 50C, which significantly contributes to the final distortion of the gear.
Gas Quenching Process Optimization
One approach for minimizing distortion was to divide the gas quenching process into stages; Figure 7(a) shows this schematically for three stages. In this manner, the gas quenching process can mimic an interrupted quench. The heat transfer rates in each stage can be controlled by changes in pressure, fan speed, or both. In this case, fan speed and application time were used. The lower bound of fan speed was 40%, and the higher bound was 100%. The heat transfer boundary conditions for both 40% and 100% fan speeds were fit using the supplied experimental data as a reference. Heat transfer coefficients and ambient temperatures for fan speeds between these speed limits were calculated using linear interpolation.
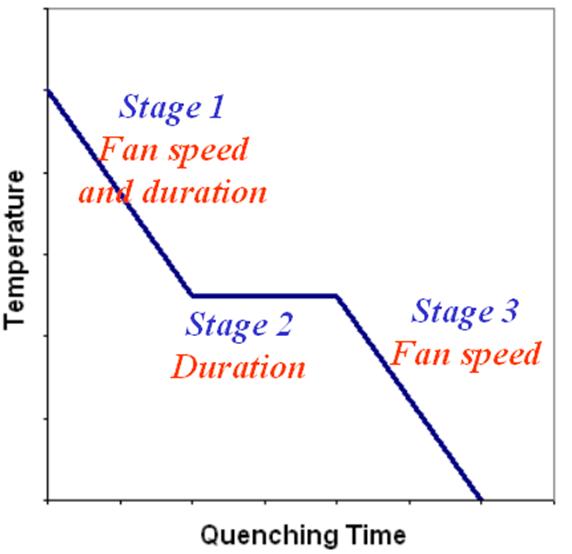
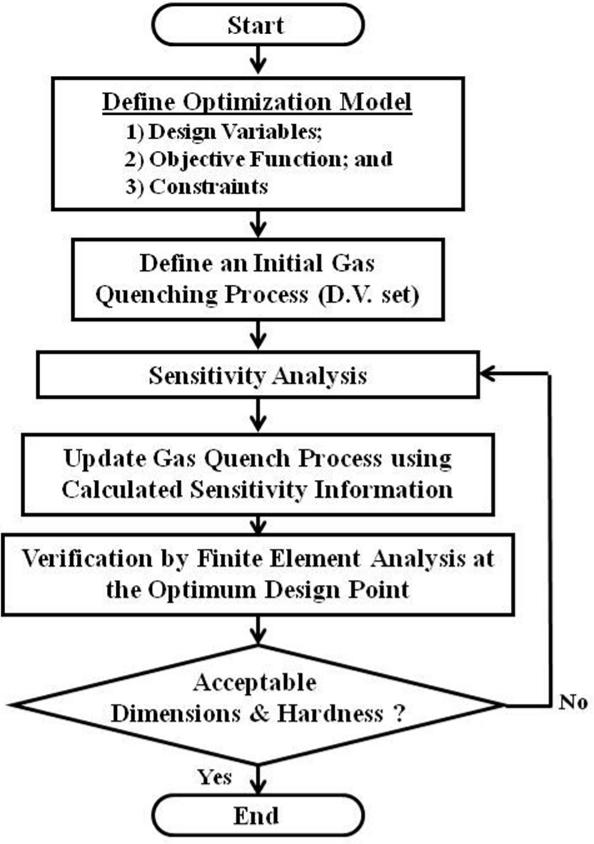
The first stage of cooling was aimed at cooling at a sufficient rate to avoid transformation to unwanted phases of pearlite and ferrite. The aim of the second stage was to use a slow fan speed to retard heat loss and allow thermal conduction within the gear to reduce any temperature differences. The third stage would then resume fast cooling, i.e. high fan speed. There are a total of four design variables (DV) in this optimization model, and they are: the fan speed of stage 1, cooling duration of stage 1, duration of stage 2, and fan speed of stage 3. The objective function is to reduce the out-of-round distortion. System constraints included the required surface and core hardness values. However, for this steel grade, the hardness requirement could be satisfied by even the slowest fan speed of 40%, so the constraints were not activated. Figure 7(b) shows the optimization strategy, where design variables, fan speed and time in this case, could be adjusted after determining from a model how that combination affected distortion. The design variables were updated for each optimization iteration using a sensitivity analysis method in an attempt to minimize distortion.
Figure 8 shows the results for the predicted effects of first stage and second stage hold times on final distortion. The graphs include results for both the 40% and 100% fan speeds in first stage cooling, and the differences are noticeable. Figure 8(a) shows that a small difference in first stage hold time difference can result in large difference in final gear distortion. For example, for a 40% fan speed in first stage cooling, a change in first stage cooling time from 22.3 seconds to 23.3 seconds is predicted to change the ring out-of-round distortion significantly from 0.12mm to 0.28mm. Similar wide variations in distortion are predicted as the first stage cooling time is increased. Large distortion differences due to a small process change indicate a process that is difficult, if not impossible, to control.
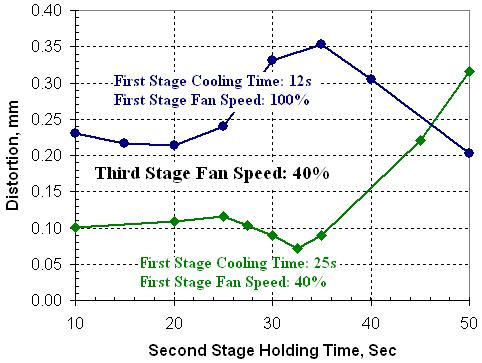
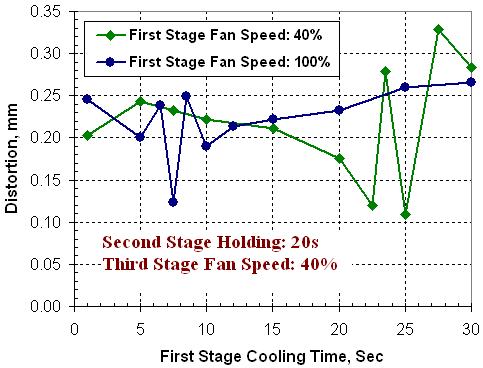
In Figure 8 (b), the effect of the hold time in stage 2 is compared for two different first stage cooling routes. For both first stage conditions, second stage hold time is predicted to affect the final distortion in a difficult to control manner. While the graph shows that a second stage holding time duration for minimum distortion can be predicted, the ability to precisely control the abrupt changes in cooling conditions in practice as opposed to in the model is doubtful.
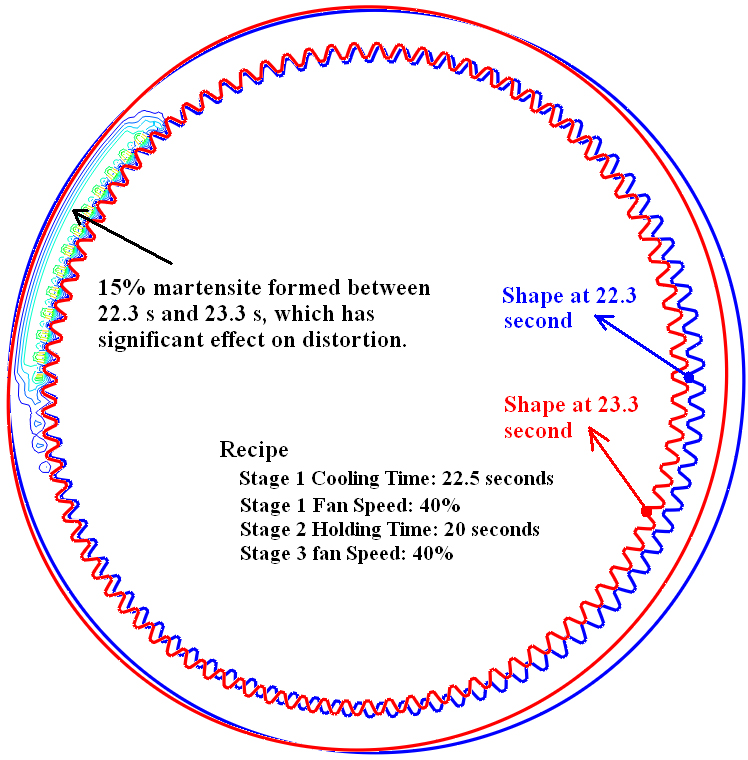
The reason for high sensitivity of distortion to the quenching process is documented in Figure 9(a). The predicted ring gear shape is shown for both 22.3 seconds and 23.3 seconds of first stage cooling. Recall that Figure 8(a) showed that these particular first stage cooling times were predicted to produce widely different final distortions. What Figure 9(a) shows is that because of non-uniform cooling, the one second of additional cooling from 22.3s (blue shape) to 23.3s (red shape) produces 15% martensite formation on one sector of the ring. This unbalanced martensite formation causes ring gear distortion to develop. Figure 9 (b) shows the final distorted rings at the end of cooling per the models reported in Figure 8(a). The out-of-round due to non-uniform cooling and resultant non-uniform phase transformation is greater for a recipe with first stage cooling that is just 1s longer than a recipe with a 22.3s first stage cooling time.
Discussion
The measured cooling curves for three locations clearly show the cooling non-uniformity that was present in this particular ring gear during 20 bar nitrogen gas quenching. The modelling attempt was to optimize the cooling practice by adjusting the fan speed and hold time for three arbitrary stages of quenching so that distortion would be minimized. By controlling fan speed and cooling time, the models predict that distortion can be minimized in theory for this geometry and steel grade. However, practical considerations suggest that the sensitivity to timing is too great to achieve success strictly by controlling fan speed and application time. Other variables need be examined to determine their effect on distortion, and how effectively they can be controlled. These other variables include gas pressure, alloy composition, and the use of gas flow deflectors or vanes to improve the uniformity of cooling.
The uniformity of cooling is a big issue for gas quenching processes. Merely eliminating a quenchant phase change does not guarantee uniformity of cooling and low distortion. In gas quenching, the uniformity of gas flow around each part in the rack is important. Also, the temperature pick-up by the gas as it circulates through the rack and removes heat from the parts is significant, as this changes the cooling power of the gas. High pressure improves heat transfer in part because the gas can extract more heat from the parts being quenched—there is more quenchant mass with increased gas pressure. Likewise, gas velocity is important to move heated gas quickly away from parts so colder gas can sustain quenching. Examination of modelling results underscores the importance of pressure, velocity, flow uniformity, and gas temperature on quenching uniformity and minimization of distortion during gas quenching.
Summary
Heat treat process simulation was used to model the vacuum carburization and high pressure gas quenching of a carburized 5130 steel ring gear. The thin walled ring gear suffered significant out-of-roundness, and modelling was performed with the intention of determining process conditions that would lessen the out-of-round distortion. For this case, the optimization methodology sought to control cooling rate and temperature uniformity so that the phase transformation of austenite to martensite would occur uniformly within the part. However, the results showed that fan speed control and timing were not sufficient alone for achieving uniform cooling. While out-of-round conditions could be improved, the process sensitivity was too great to achieve a practical recipe that would produce consistent results. Other variables must be included in the drive for greater uniformity of quenching.
Although not presented in this paper, the included thermocouple data and the additional thermocouple data directly show the non-uniformity in quenching this rack of ring gears. Computational fluid dynamics modelling of the quenching process would be a welcome step in better understanding gas quenching and in providing directions for process improvement.
References
- B. Lynn Ferguson, Andrew M. Freborg, Greg Petrus and Melvin L. Callabresi, “Predicting the Heat-Treat Response of a Carburized Helical Gear,” Gear Technology, v19 (6), p20-25, Nov-Dec 2002.
- B. Lynn Ferguson, and W. Dowling, “Predictive Model and Methodology for Heat Treatment Distortion,” NCMS Report #0383RE97, 1997.
- Iwata Hitoshi, “Advanced Acetylene Vacuum Carburizing,” IHI Engineering Review, v38 (2), p83-88, August, 2005.
- Zhichao Li, Ramana Grandhi, and Raghavan Srinivasan, “Distortion Minimization during Gas Quenching Process,” Journal of Materials Processing Technology, v172, p249-257, 2006.