
Liquid quenching of long steel components can introduce significant distortion if the component is not lowered into the liquid quench bath properly. Whether the liquid quenchant is oil, water, or a polymer solution, the angle and rate of immersion can have a significant effect on the final distortion. Heat-treatment simulation software can provide insight into how a long component will behave during heat-treatment, but only if the immersion process is simulated. The simulation of relatively small steel components assumes that the entire part enters the quench bath simultaneously. This assumption is valid for most bearing rings, gears, etc., since the entire part is submerged within the quenchant in a fraction of a second. However, the assumption begins to lose its validity when applied to relatively long parts.
To show the significance of simulating the immersion process during quench hardening of relatively long steel components, a 500 mm long, 12 mm diameter steel bar made of AISI 9310 was constructed and meshed in Ansys, and the heat-treatment process was modeled using the heat-treatment simulation software DANTE. DANTE is a series of material subroutines, linking to the finite-element solvers Ansys or Abaqus, used to predict microstructural evolution, in-process and residual stress, deformation, and hardness of steel components subjected to a heat-treating process. DANTE also has the capability to model the immersion process.
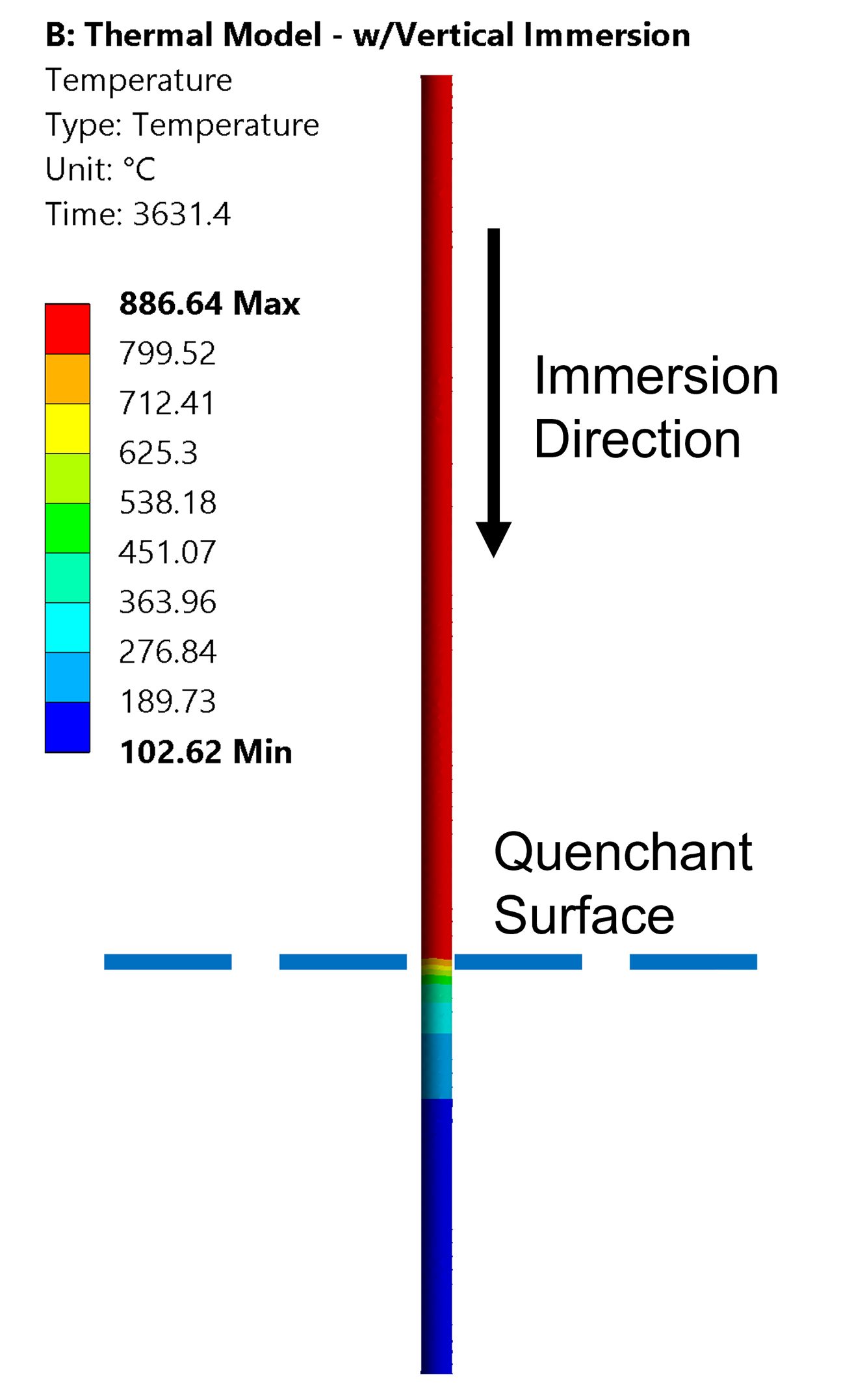
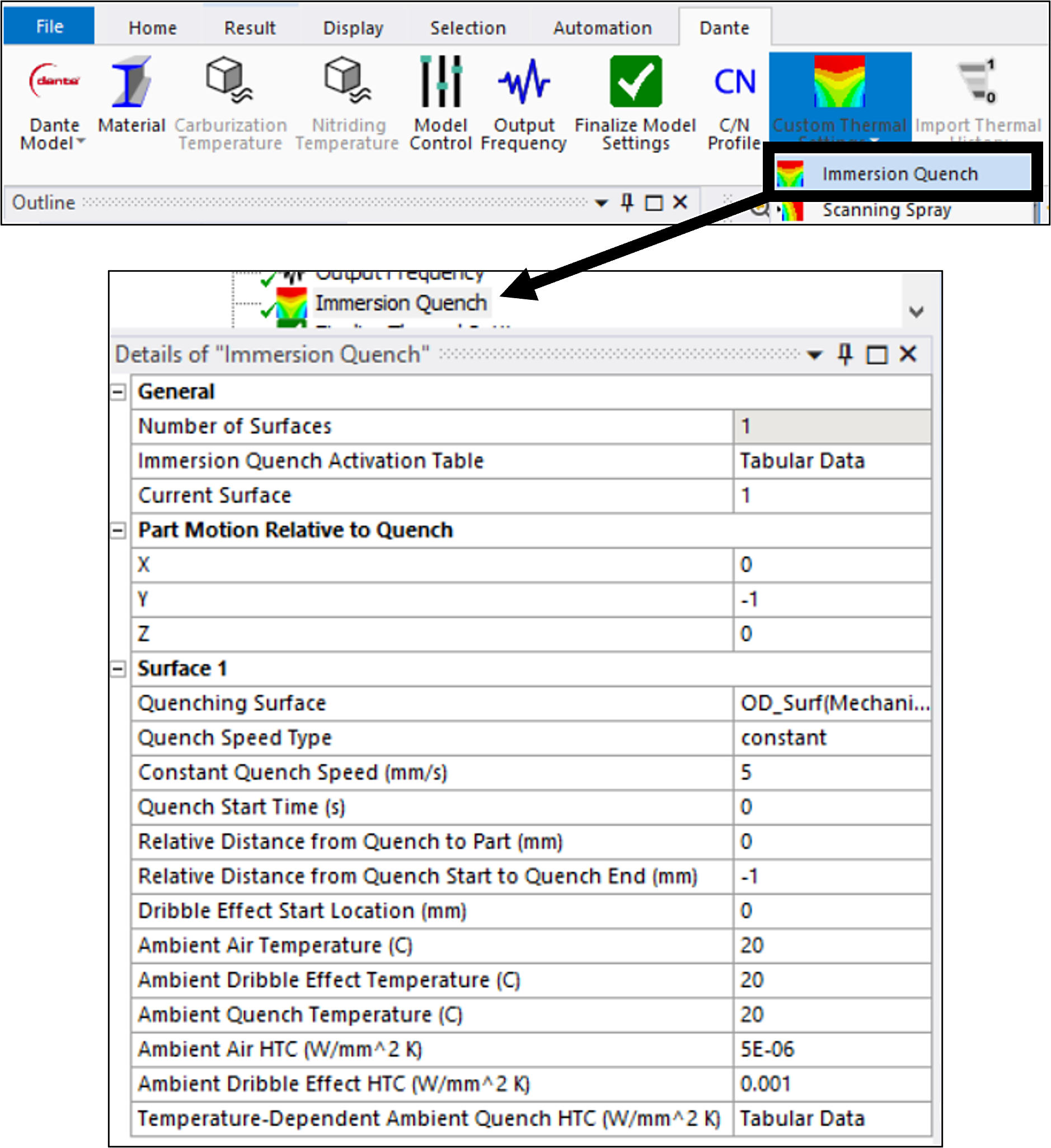
An algorithm in DANTE determines the location of the component relative to the quenchant surface, as shown schematically in Figure 1, and applies a defined air heat transfer coefficient (HTC) to the part surface above the quenchant surface and a defined liquid HTC to the part surface below the quenchant surface. An immersion object from DANTE linking with Ansys is added to the simulation and the immersion parameters are defined, as shown in Figure 2. Parameters include immersion orientation, immersion rate, and HTCs to describe the conditions inside and outside of the quenchant. Outside of the quenchant, the air HTC is defined as a constant. This is a valid assumption given the relatively small temperature changes experienced by the surfaces not exposed to the liquid quenchant. The liquid quenchant, on the other hand, can, and must be, defined as a function of part surface temperature. The liquid quenchant HTC must be defined as such to capture the change in cooling power of the three stages of liquid quenching: vapor blanket, nucleate boiling, and convection. Figure 3 shows the HTC versus part surface temperature for all of the simulations described in this article.

The simple case study described in this article is used to show the importance of modeling the immersion process, with both processes, with and without simulating the immersion process, using the same temperatures, HTCs, and times. One process assumes that the entire length of the bar was immediately placed in the quenchant, i.e., without immersion. The other process assumes the component was immersed into the quenchant at a rate of 5 mm/s, i.e., with immersion. The axis of the bar lies along the global Y-axis in the model. Figure 4(A) shows the distortion prediction in the X-direction for the no immersion model and Figure 4(B) shows the prediction for the immersion model.
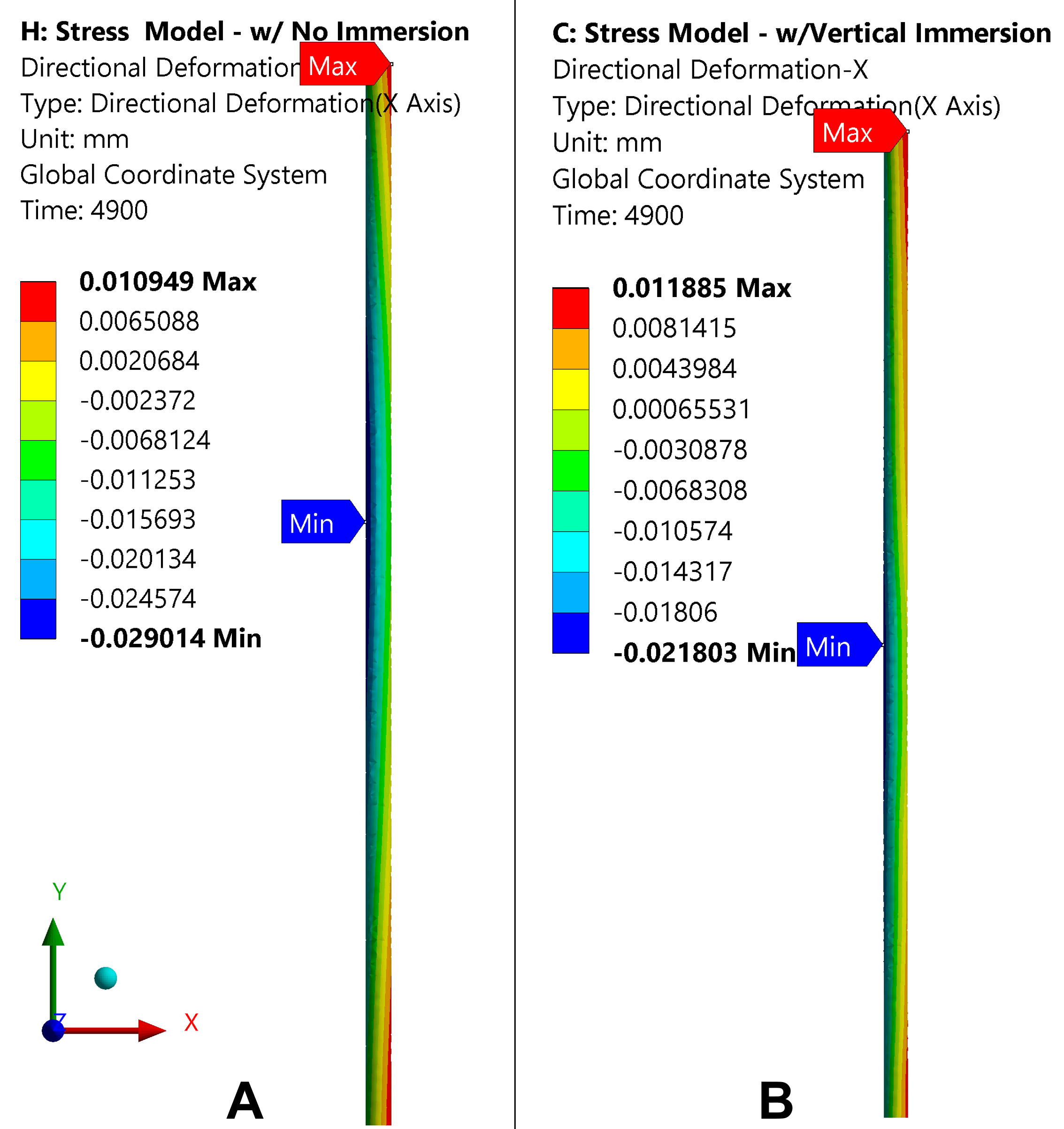
In the X-direction, the distortion is equivalent in both magnitude and direction, which is due to the change in cooling rate near the ends of the bar. As the bar diameter is increased, conduction becomes the limiting factor in the transfer of thermal energy, reducing the distortion effects from end cooling. However, the results in the Z-direction tell a much different story, as shown in Figure 5. In the Z-direction, the first thing to notice is the bow predicted by the immersion model, Figure 5B, is twice as large as the model that assumed no immersion, Figure 5A — 40 µm for the no immersion model, compared to 80 µm for the immersion model. The next thing to notice is the direction of the bows between the two models; they are in opposite directions. This is a common phenomenon witnessed by DANTE Solutions after many years of modeling these types of components and process.
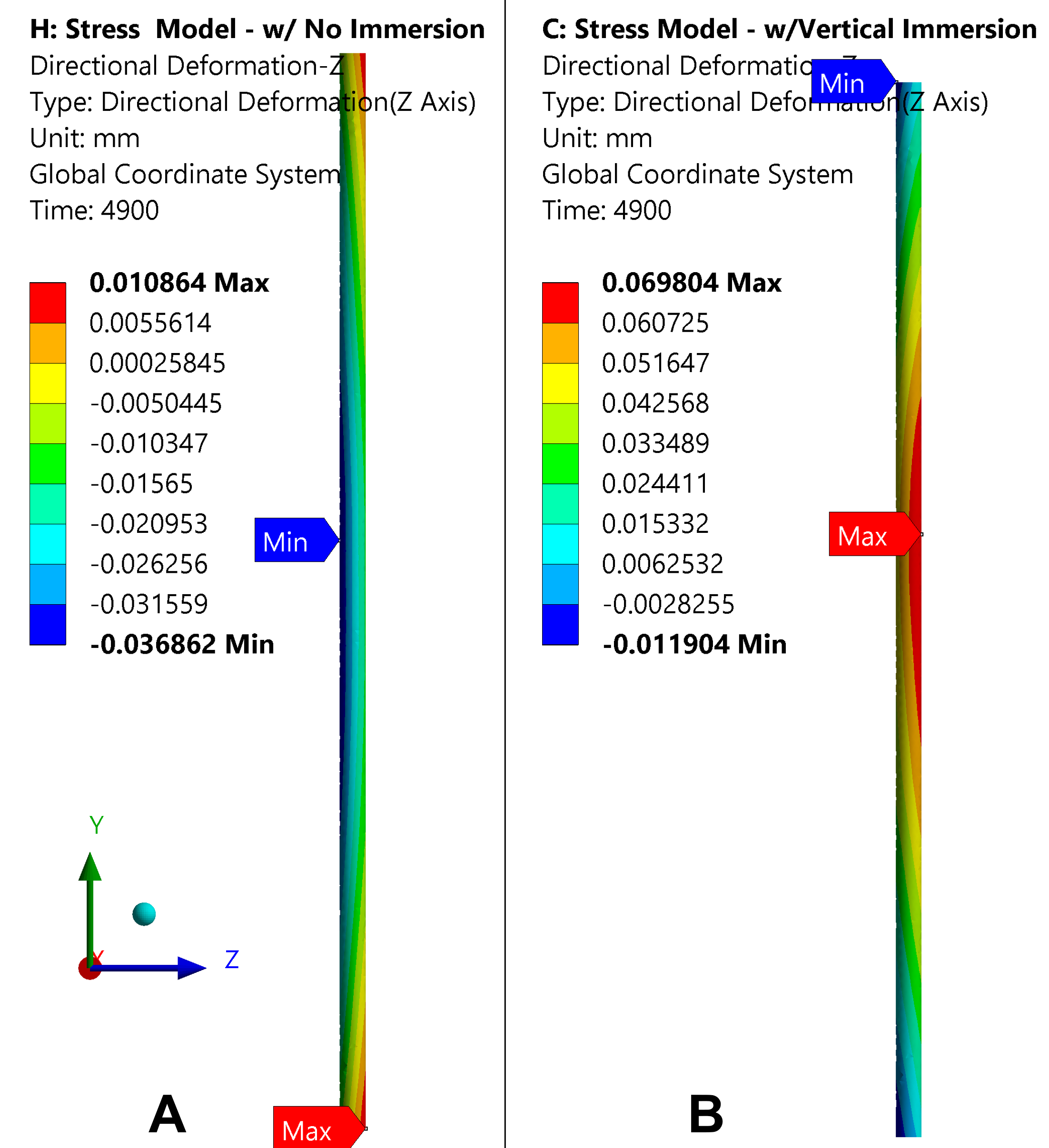
It is interesting to note that the distortion in the X- and Z-directions for the no immersion model are equivalent, as shown in Figures 4A and 5A. Again, this is due to the difference in cooling behavior close to the ends of the bar. The final direction to evaluate the distortion is the axial length of the bar, which is also approximately equivalent between the two models as shown in Figure 6. This is as expected, since most of the axial distortion is created by the volume difference between the initial and final microstructure of the steel alloy. However, if the bow distortion is the same magnitude as the axial distortion, then the two methods of simulation may not be equivalent in the axial length of the bar; the bow distortion for the case described here is a full magnitude less than the axial distortion. All types of behavior described are dependent on geometry and process parameters and should not be taken as general rules.
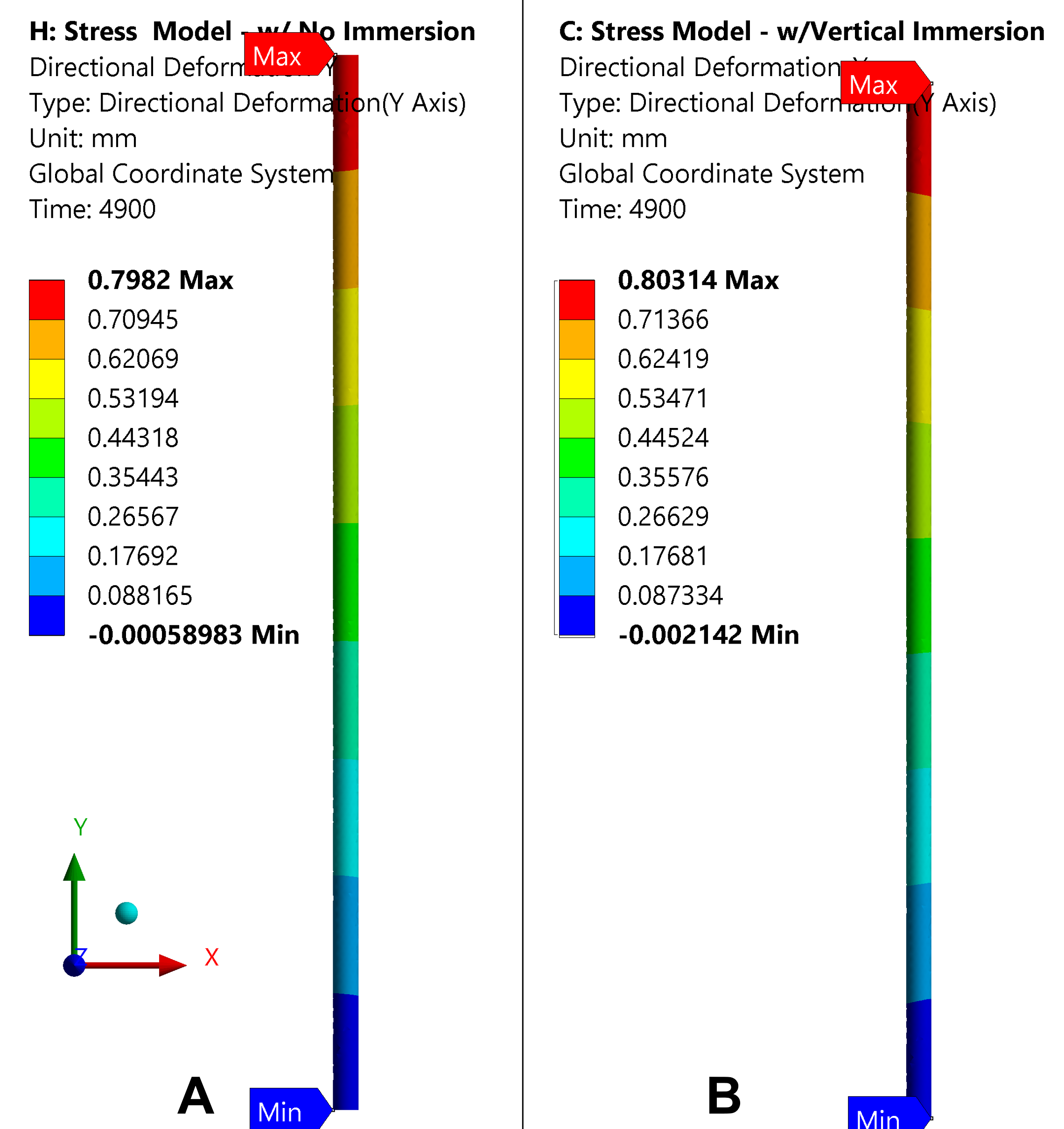
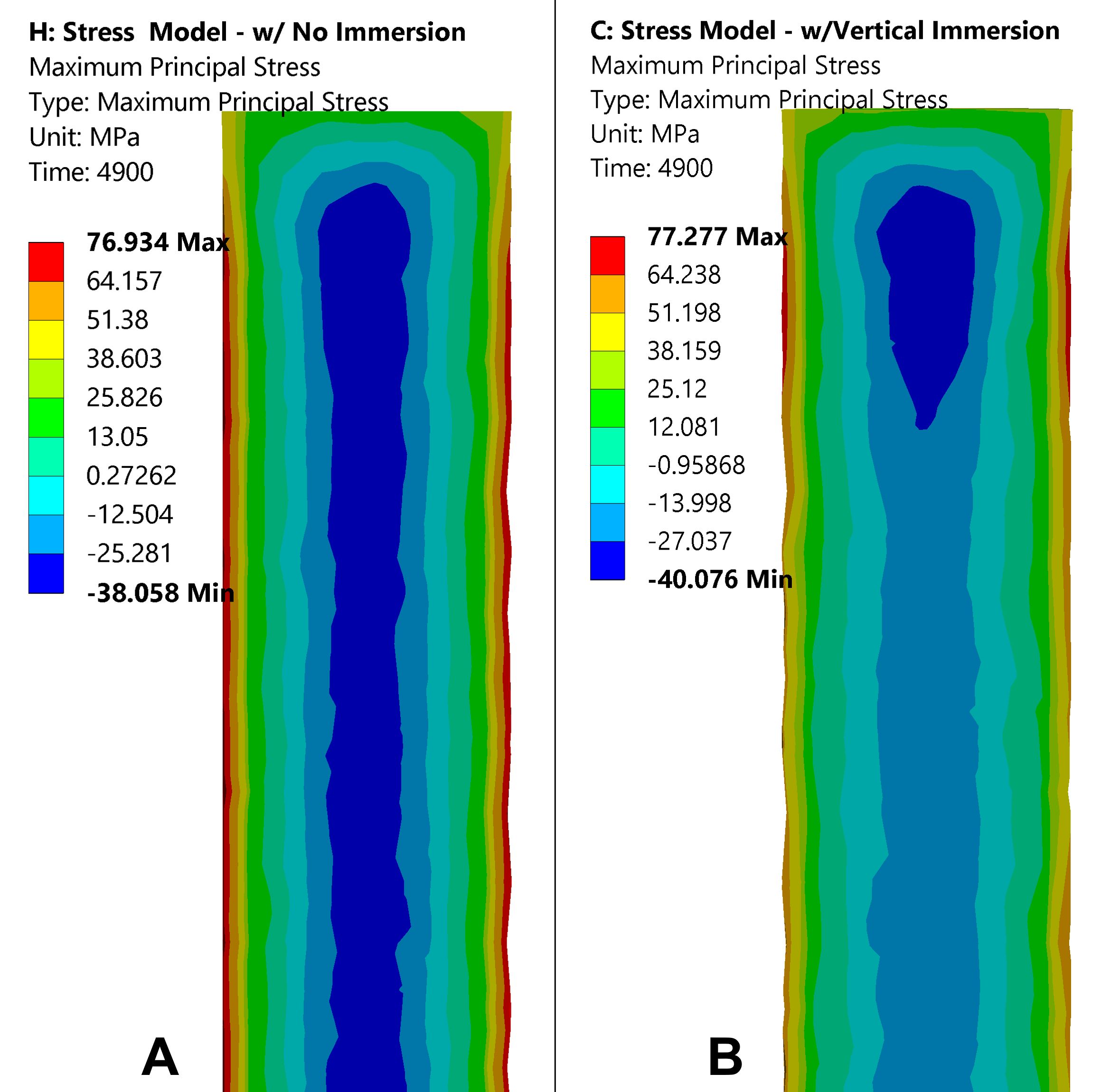
Interestingly, although the distortion is different between the two simulation methods, the residual stress present in the part at the end of quenching is equivalent. Figure 7 shows the residual stress predictions at the end of quenching for the case considering (A) no immersion and (B) immersion. This is due to the bulk of the residual stress being formed from the volumetric change of the material as it transitions from austenite to its final microstructural phase after quenching to room temperature, which is martensite for this case. This equivalency is only present due to an equivalence between the two microstructures. If the immersion process causes a diffusive phase to form at one end of the bar and not the other, the residual stress will be different given the modeling method.
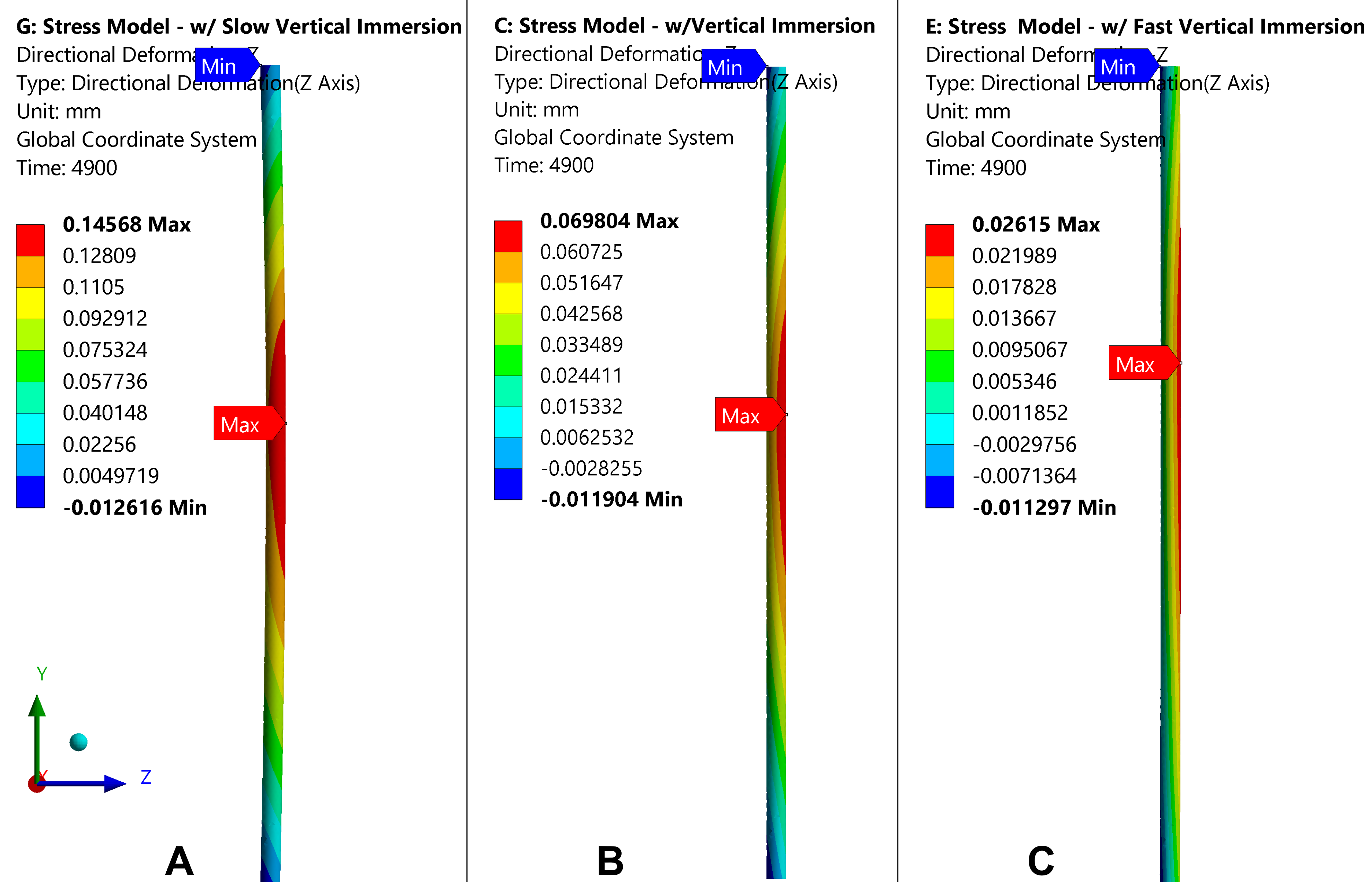
DANTE also has the capability to model the quench rate as a constant or as a function of time, which will generally alter the distortion of the component. Figure 8 shows the DANTE predictions for the distortion in the Z-direction for three constant immersion speeds: 2.5, 5, and 10 mm/s. As can be seen, the slower immersion rate produces the greatest amount of bow distortion — 160 µm for the slowest immersion rate, 80 µm for the medium rate, and 40 µm for the fastest immersion rate. This is generally true; a slower immersion rate will generate greater distortion, though not always. The same is true of component diameter: the smaller the diameter, the greater the distortion. While these two statements are generally true, heat-treatment distortion can be a nonlinear phenomenon, with distortion sometimes not behaving intuitively. The nonintuitive nature of heat-treatment distortion makes simulation of the process even more important.
In summary, it was shown that to accurately simulate the liquid quenching of long components, the immersion process must also be simulated. If the immersion process is ignored, not only can the distortion magnitude be inaccurate, but the distortion mode may be incorrect. The immersion rate was also shown to play a critical role in the distortion magnitude. The heat-treatment simulation software DANTE has the capability to simulate the immersion process and help design a better quenching process for long components.

























