In a total of nine experiments, the optimization of heat-treatment parameters of medium carbon steel quenched in different media was conducted using the Taguchi method and Grey relational analysis.

Quenching is one of the major processes of heat treatment of medium carbon steel that aims at improving its mechanical properties. However, the effectiveness of this process is dependent on several control factors that must be maximized to obtain optimum results in terms of hardness, yield strength, and ultimate tensile strength, among others. This study aims at optimizing the process of improving the mechanical properties of medium carbon steel by varying some key factors such as the quenchant used (A), heat-treatment temperature (B), and soaking time (C). The measured responses in this study were the hardness, yield strength (YS), and ultimate tensile strength (UTS).

Optimization was conducted in two stages: The first stage dealt with the mono-optimization of process parameters using Taguchi’s Signal-to-Noise (S/N) ratio. A total of nine experiments were performed based on standard L9 orthogonal array because each of the three control factors has three levels. The second stage was a multi-objective optimization using Taguchi-based grey relational analysis (GRA). The optimal conditions for hardness, YS, and UTS were obtained at A2B3C3, A3B2C3, and A3B3C3, respectively. Using ANOVA as statistical analysis, it was observed that the soaking time was the main control factor for all three measured responses (31.95% contribution ratio for hardness, 62.46%, and 66.76% for YS and UTS, respectively), while the quenchant had the least contribution. Analysis of the Taguchi-based GRA revealed that the results obtained are in total conformance to that of the Taguchi method, with soaking time having the highest contribution ratio of 69.41%.

1 Introduction

Heat treatment is a property enhancement process that deals with the heating and cooling of metal in a solid-state. The objective of heat treatment is to impart certain desirable properties on metals (Ahaneku et al., 2012). Heat treatment can be performed on metals, ceramics, and composite material. Heat-treated materials undergo phase, microstructural, crystallographic, and phase transformation (Sreeja et al., 2016). The major aim of heat treatment is to enhance the mechanical properties of steel such as hardness, yield strength, tensile strength, ductility, and impact resistance. Heat treatment of steel involves the combination of controlled heating and cooling operations (Adeleke et al., 2019). The cooling process could be achieved by allowing the heated material to cool slowly under natural air or by dipping it in a quenchant. As reported by Ikubanni et al. (2017), quenching is a major process of heat treatment in enhancing the properties of carbon steel. Quenching is carried out to disallow the formation of ferrite or pearlite but to support the formation of bainite or martensite. Oil is a major quenchant (quenching medium), which consists of water, aqueous polymer solution, and various additives. Owing to the importance of quenching in the heat treatment process, several researchers had previously used different kinds of quenching media to improve the properties of steels (Adeleke et al., 2018; Ikubanni et al. 2017, 2018; Adekunle et al., 2013; Odusote et al., 2012; Ndaliman, 2006).

The Taguchi method was first used in 1987 by Genichi Taguchi. It is one of the prominent optimization and statistical tools used in ranking the importance of different factors for a target function (Taguchi, 1987). Though the method was majorly applicable in experimental analysis, it could also be used in theoretical and numerical analysis (Hu et al., 2018; Naqiuddin et al., 2018; Arslanoglu and Yigit, 2017; Bao et al., 2013). In the study of Ikubanni et al. (2017), quenching media, heating temperature, and soaking time were identified as the major process parameters in the heat treatment of medium carbon steel (MCS). The mechanical properties evaluated were hardness, yield strength, and ultimate tensile strength. However, to optimize these process parameters, a further study involving the use of Taguchi analysis as well as Grey Relational Analysis (GRA) is required to be carried out. The Taguchi method allows a fewer number of experimental tests because it uses orthogonal arrays to minimize the effects of noise factors (Palanikumar, 2011; Taguchi and Konishi, 1987). The Taguchi method uses a loss function to determine the deviation between the experimental results and the desired values. This loss function is further converted into Signal-Noise (S/N) ratio (Asilturk and Akkus, 2011). There are three types of quality characteristics in the analysis of S/N ratio: the lower-the-better, the nominal-the-best, and the higher-the-better (Gupta et al., 2011; Gunes et al., 2011; Liu et al., 2009; Jun et al., 2005).

Though Taguchi is a powerful optimization tool, it is not a suitable method for the simultaneous optimization of multi-objective functions (Canbolat et al., 2019). Therefore, GRA was applied to the mechanical properties of MCS to obtain the order (rank) of the importance of each process factor by maximizing the hardness, YS, and UTS of MCS. The concept of the Taguchi design of experiment, which is now applicable in all fields of research was first introduced in agriculture. According to Turgay (2014), the Taguchi method has been widely used in engineering applications such as design, analysis, engineering management, and so on. Hussein et al. (2018) optimized the heat-treatment parameters for the tensile properties of medium carbon steel. The optimal factors of heat treatment such as tempering temperature, nanoparticles percentage, base media type, nanoparticles type, and tempering time that would increase the yield strength, ultimate tensile strength, and ductility of the MCS were determined using the Taguchi technique. In manufacturing processes, Kumar and Singh (2019) optimized the rotary ultrasonic drilling of BK-17 optical glass using the Taguchi method and utility approach. The study focused on enhancing the machining efficacy by simultaneous optimization of conflicting target functions using utility approach. The L9 orthogonal array was adopted for the experimental work. Feed rate, rotational speed of the tool, and ultrasonic power were selected as process parameters to evaluate their effects on the material removal rate and surface roughness.

Several studies have been done in the utilization of combined Taguchi-based and GRA methods in optimizing different processes. For instance, the milling characteristic was optimized using Taguchi-based GRA by Sarikaya et al. (2016). The effects of the process parameters such as depth of cut, feed rate, cutting speed, and the number of inserts on the cutting force, vibration, and surface roughness were investigated. The findings revealed the optimum conditions were achieved at the depth of cut of 1 mm, feed rate of 0.05 mm/rev, cutting speed of 308 m/min, and the number of insert of 1. A similar study was conducted by Meral et al. (2019) to optimize the characteristic of the hole drilled by novel drill geometries. In this study, the selected input parameters were drill geometries, cutting speed, and feed rate; while the measured responses were drilling torque, thrust force, and surface roughness. It was concluded that the desired surface roughness and thrust force were obtained with the geometry 4.

Nguyen et al. (2020) and Muthuramalingam et al. (2020) also adopted Tagugi-based GRA in the electrical discharge machining (EDM) process. In their study, Nguyen et al. (2020) chose peak current, pulse off time, pulse on time, and gap voltage as controllable factors. Responses such as average surface roughness, material removal rates, average layer thickness, and microhardness were obtained based on the selected controllable factors. Also, in the wire EDM process, Muthuramalingam  et al. (2020) affirmed the selection of the wire electrode was the main factor that affects the quality measures in the wire EDM process, owing to its ability to create the energy required for a spark. In energy studies, the Taguchi method together with the GRA was used in a sizeable number of researches such as the use of the Taguchi method and GRA on a tubulated heat exchanger (Celik et al., 2018); multi-response optimization of geometric and flow parameters in a heat exchanger tube with perforated disk inserts by Taguchi grey relational analysis (Chamoli et al., 2016); and flat-plate collector process optimization with multiple quality characteristics in solar energy collector manufacturing (Kuo et al., 2011).

From the available literature, little or no study has been conducted on the application of the Taguchi-based method with GRA technique on the optimization of heat-treatment parameters of MCS. Therefore, this study aims at optimizing process parameters for the enhancement of the mechanical properties of MCS by using liquids that could have been termed as wastes such as engine oil (spent), coconut, and pap water as quenchants. The study optimized the responses such as hardness, yield strength, and ultimate tensile strength of heat-treated MCS by adopting the higher-the-better characteristics. The mono-objective optimization was done via Taguchi’s S/N analysis while Taguchi-based gray relational analysis was used for the multi-objective optimization of the responses.

2 Materials and experimental method

2.1 Specimen preparation, heat treatment, and quenching

The sample used in this study is a medium carbon steel (MCS) obtained from Omu-Aran metropolis market, Nigeria. The chemical composition of the MCS is as shown in Table 1.

Table 1: Chemical composition of the medium carbon steel.

Quenchants used were coconut water (CW), pap water (PW), and spent engine oil (SPE). With the aid of a medium-size lathe machine, specimens for hardness testing and tensile testing were prepared from MCS following ASTM standards. For induced stress reduction during machining, metallurgical re-conditioning, phase re-adjustment, and homogenous structure, the specimens prepared were initially heat-treated to a temperature of 840°C using a muffle furnace and normalized. The prepared specimens were later heated in a muffle furnace to 730, 760, and 790°C, and soaked for 30, 45, and 60 minutes, respectively. After, the samples were quenched in the different quenchants (CW, PW, and SPE). Mechanical tests such as hardness and tensile tests were later conducted on the quenched samples.

2.1.1 Hardness test

Brinell hardness tester (EEDB 0006/43, Edibon) was used in determining the hardness values of the samples base on the ASTM E10-18 standard. A load of 500 N was used to cause an indent on the samples using a ball indenter. The dwelling time of 15 seconds was used. The indented diameter value was obtained. Equation 1 was employed to evaluate the Brinell’s hardness number (BHN) for each sample. The average value of the BHN was recorded after triplicates hardness tests were done on each sample.

where:

F is the Force (N).

D is the indenter’s diameter (mm).

d is the average indentation’s diameters (mm).

2.1.2 Tensile test

Tensile testing was done on a Testometric machine (M500-50AT model) based on the ASTM E8 standard. The tensile test specimen was loaded until it fractured. Recording of the gauge lengths of the samples was done before applying load. The yield and tensile strengths of each sample were also estimated from the generated data.

2.2 Experimental design and optimization

2.2.1 Taguchi method and design of experiment

The experimental design followed the Taguchi method to obtain the ranking of importance of different process parameters for the target functions (responses). In this study, the three  process parameters considered are quenchant, heating temperature, and soaking time. The three levels for each factor chosen are shown in Table 2.

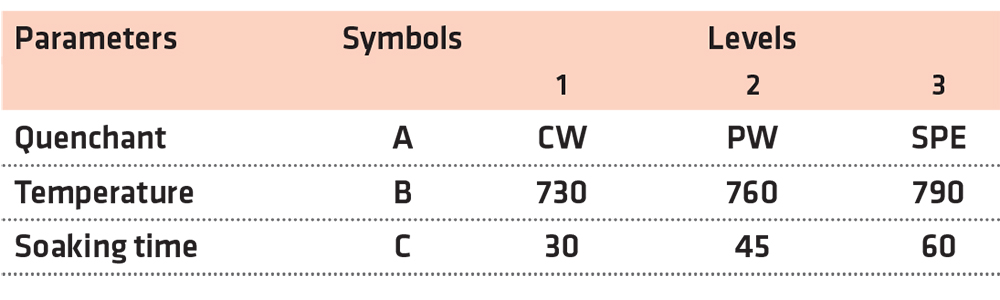
Table 2: The three process parameters and their levels.

The Taguchi method was applied to the heat-treatment process in this study to maximize the hardness, YS, and UTS of MCS. The L9 orthogonal array was chosen to allow the three process parameters at the three different levels considered (Table 2). In the Taguchi analysis, the values of the responses were transformed into signal-to-noise (S/N) ratios. Since all three responses (hardness, YS, and UTS) were desired to be maximum, the higher-the-better performance characteristics for calculating the S/N ratio was chosen in this study by using Equation 2.

where:

n is the number of replication for each experiment.

yi described the result value for the ith performance characteristics.

2.2.2 Analysis of variance (ANOVA)

ANOVA is a statistical tool used in determining the individual interactions and the contribution ratio of all the parameters in the experimental design. ANOVA was used to analyze the effects of quenchant, heating temperature, and soaking time on the hardness, YS, and UTS of the MCS. Since ANOVA highlights the importance order of influencing parameters on the response, it helps in validating the results obtained through the Taguchi method. In this study, Minitab 19 (Statistical software) was used for both ANOVA and Taguchi analysis.

2.2.3 Confirmation test

After establishing the optimum values of hardness (Hdopt ), yield strength (YSopt), and ultimate tensile strength (UTSopt) using the Taguchi method, a confirmation test was conducted to validate the optimum conditions (Mandal et al., 2011). Optimum values of the responses were estimated using Equations 3, 4, and 5:

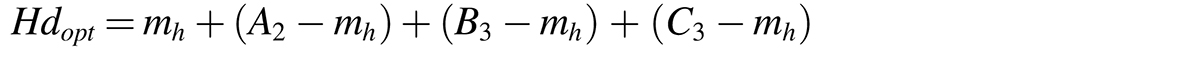
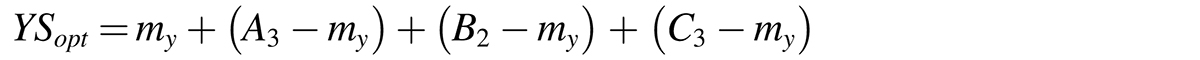
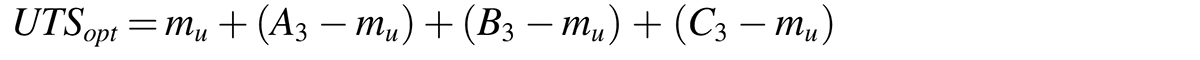where (A2B3C3), (A3B3C2), (A3B3C3) represent the values of the optimum level of hardness, yield strength, and ultimate tensile strength respectively. mh, my, and mu are the average of all the Hdopt , YSopt , and UTSopt , respectively, obtained from the experimental study.

To determine if the optimum values of the responses agree with the experimental values, confidence intervals (CI) were calculated for each response (Dvivedi and Kumar, 2007) using Equations 6 and 7.

where

Fα,1,fe = F ratio at a 95% confidence.

α = significance level.

fe is the degrees-of-freedom of error.

Ve = variance’s error.

neff = effective number of replications.

R = number of confirmation experiments’ replication.

N = total number of experiments.

Tdof is the total main parameters degrees of freedom.

2.2.4 Grey relational analysis (GRA)

Taguchi is an unsuitable method for the simultaneous optimization of multiple-objective functions. Hence, the GRA method was applied to achieve the ranking of importance of each process parameter on multiple performance characteristics by maximizing all the responses (hardness, yield strength, and ultimate tensile strength) simultaneously.

First, the experimental results were normalized (usually in the range of 0-1). The higher-the-better performance characteristic in Equation 8 was used for all the target functions because the maximum values of all the three responses are desired.

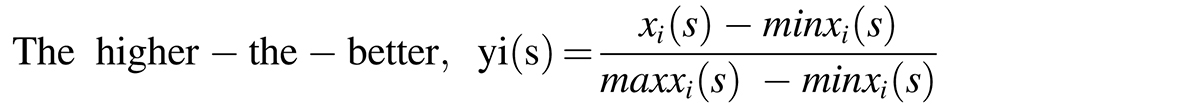After normalization, the grey relational coefficient is calculated using Equations 9 and 10

where Δoi(s) is the deviation sequence calculated from Equation 10

xi(s) is the comparability sequence, max xi(s) and min xi(s) are maximum and minimum  comparability sequence respectively, xo(s) is the referential sequence, φ is the identification coefficient, which ranges from 0 to 1. In GRA, using any value between 0 and 1 for φ would not change the order of importance of the parameters but 0.5 is normally chosen (Naqiuddin et al., 2018; Acir et al., 2017; Chamoli et al., 2016; Turgut et al., 2012; Kuo et al., 2011; Tosun, 2006).

The grey relational grade (GRG) was then estimated by using Equation 11 before the final ranking was done.

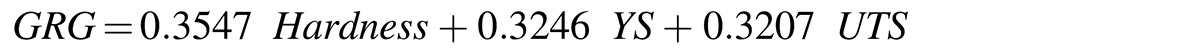3 Results and discussion

3.1 Analysis of the signal-to-noise ratio (S/N)

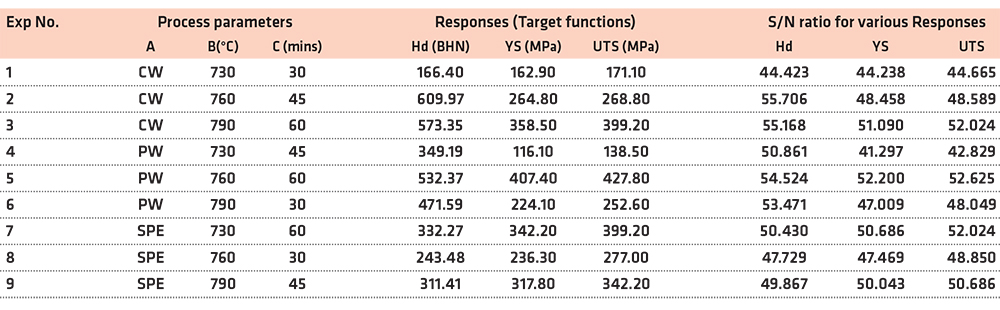
The hardness (Hd), yield strength (YS), and ultimate tensile strength (UTS), which are the responses (target functions) of the MCS, are displayed in Table 3. Table 3 also presents the S/N ratios for the various responses.

Table 3: Experimental results and their S/N ratios.
3.1.1 Analysis of a response (Hardness)

The average S/N ratios and the ranking of the importance of process parameters on the hardness value (Table 4). Figure 1 represents the main effect of each parameter on the hardness of the MCS.

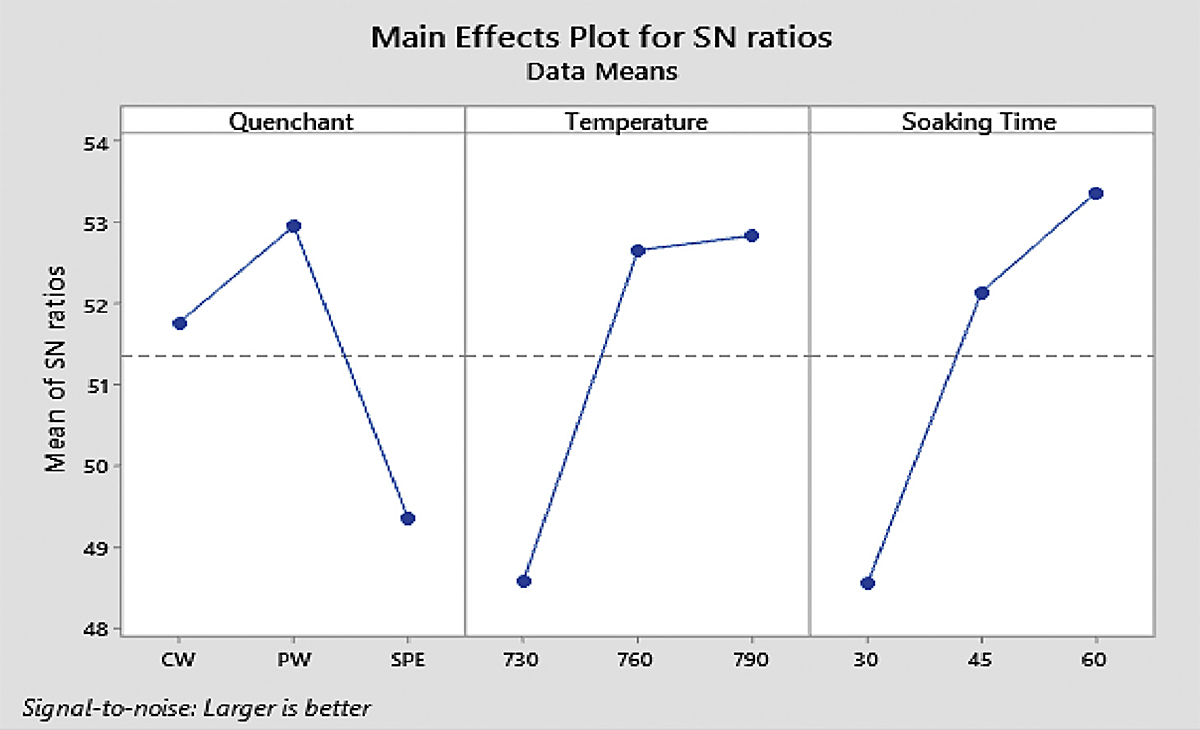
Table 4: Response for S/N ratios (hardness vs. quenchant, temperature, and soaking time).
Figure 1: The main effect plots for S/N ratios on hardness (Taguchi).

According to Canbolat et al. (2019), when the highest and lowest S/N ratios variation is small, it implies there is a relatively low effect of the parameter on the response. More so, the design parameters level with maximum S/N indicates the optimum conditions of the system. Hence, the process parameters to obtain the optimum values for maximum hardness are determined as Quenchant = PW, Temperature 790°C, and Soaking time = 60 minutes (Figure 1). This implies that when the heat treatment is done in PW at a heating temperature of 790°C with a soaking time of 60 minutes, i.e. A2B3C3, the highest hardness can be obtained. Therefore, the optimum hardness from the operating condition range of this study is found when the heat-treatment process was done under the optimum working condition (A2B3C3). This agrees with the study of Ikubanni et al. (2017), which opined that CW and PW could be used as quenchants when improving the hardness of MCS.

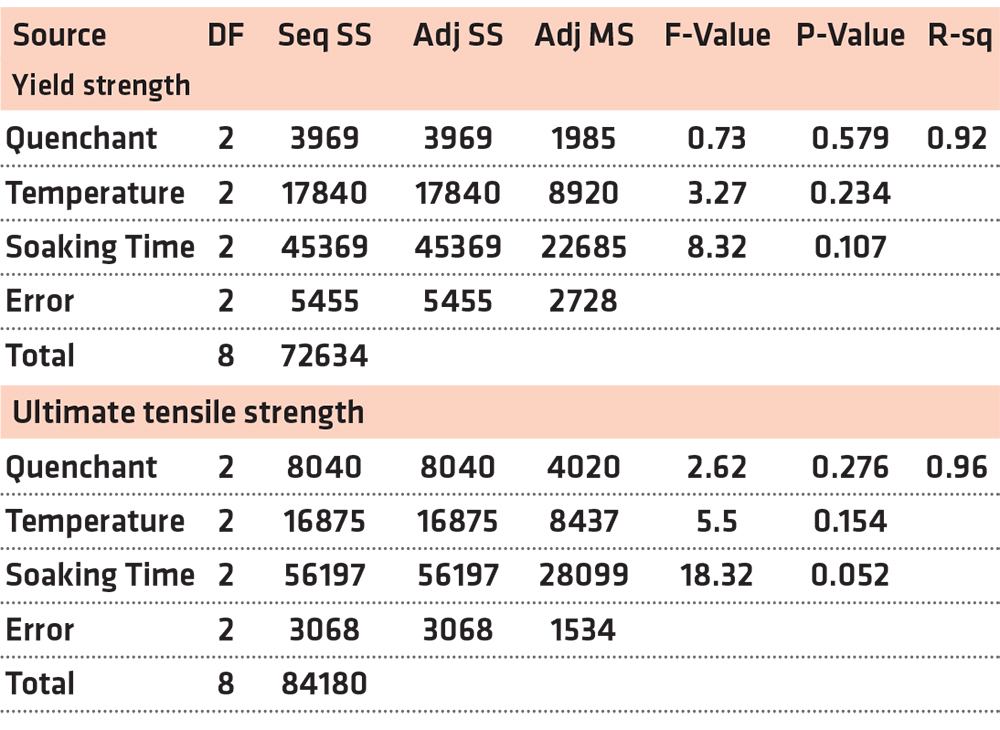
For the results to be statistically reliable, the ANOVA method was used to validate the Taguchi analysis results (Sarikaya and Güllü, 2014). This is done to estimate the percentage contribution of each parameter of the heat-treated samples in the different media on the hardness property of the MCS. The usage of the ANOVA shows the impacts of process parameters on the hardness, as shown in Table 5 and Figure 2.

Table 5: ANOVA results on the hardness of MCS.
Figure 2: Contribution ratio of each process parameter on the hardness of MCS (ANOVA).

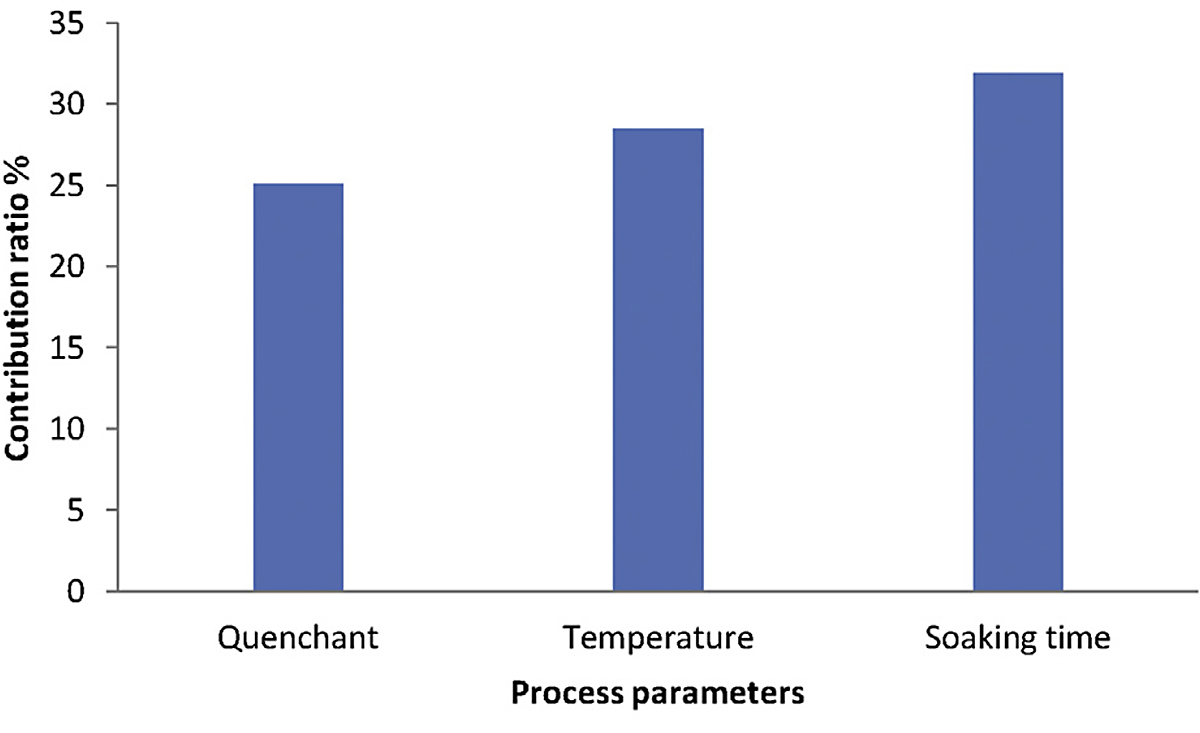
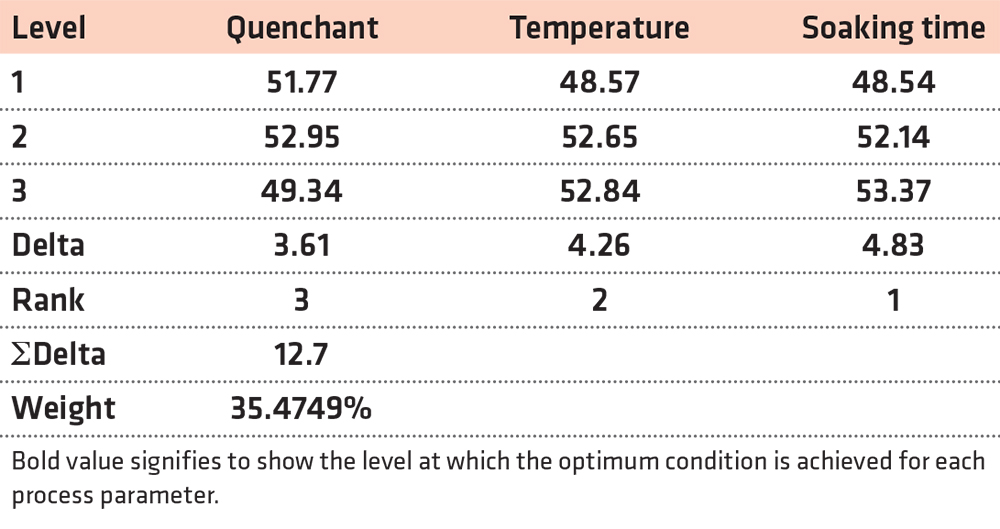
Soaking time was observed to be the major process parameter on the hardness of the heat-treated MCS with an impact ratio of 31.95% based on the ANOVA results. Contribution ratios, shown in Table 4, also indicates that the ranking of the importance of the process parameters on the hardness of the MCS was Soaking time > Temperature > Quenchant. The main effect plots of the Taguchi method and the ANOVA results gave a similar ranking of the effect of the process parameters on the hardness of MCS. The results in the present study affirm the report of Singh et al. (2013) on the effect of soaking time on the behavior of carburized mild steel, where it was stated that the soaking time increment has a direct influence on the hardness value increment of the mild steel used. It was similarly reported by Valdes-Tabernero et al. (2019) that fraction of the recrystallization ferritic matrix with embedded martensitic and retained austenite grains generally tends to increase with increasing soaking time, thus, the tendency of an increased hardness in mild carbon steel. Therefore, an increase in soaking time above all other process parameters during the heat treatment of MCS has the largest impact on its hardness.

3.1.2 Analysis of target functions (Yield strength and ultimate tensile strength)

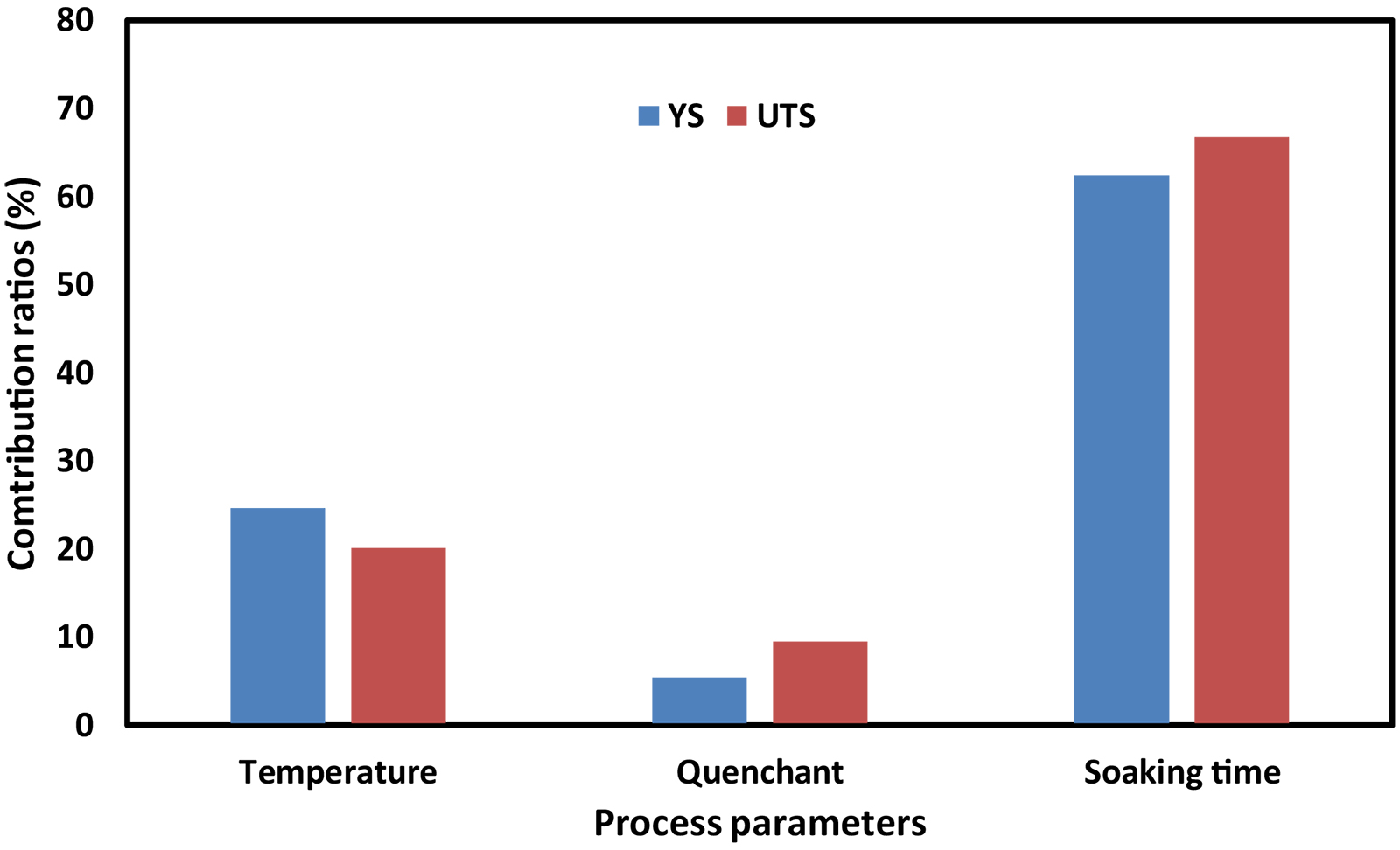
Table 6 shows the average S/N ratios and the rank of the importance of the process parameters on the values of YS and UTS. Figures 3 and 4 represent the effect of each parameter on the YS and UTS, respectively. It can be observed from Table 6 that soaking time was ranked first with a higher influence on the yield strength of the heat-treated MCS among the three process parameters that were considered. Similarly, Table 6 shows that soaking time, which was constantly ahead of temperature, had the highest influence on the ultimate tensile strength of the heat-treated MCS. The use of SPE as quenchant while operating at 760°C and soaking for 60 minutes was the optimum values of the process parameters for which the maximum YS, as shown in Figure 3 (A3B2C3). While the soaking (60 minutes) and the quenchant (SPE) were unchanged as the optimum values as process parameters to obtain optimum ultimate tensile strength for the treated MCS, the temperature changed from 760 to 790°C, as shown in Figure 4. The maximum UTS was obtained when the heat treatment was done under the optimum working condition (A3B3C3). The ANOVA results of the effects of various process parameters on the YS and UTS are presented in Table 7, while the contribution ratios are presented in Figure 5. This corroborates the study of Ikubanni et al. (2017).

Table 6: Response for S/N ratios (YS and UTS vs quenchant, temperature, and soaking time).
Figure 3: Main effect for S/N ratio of each parameter on yield strength (Taguchi).
Figure 4: Main effect for S/N ratio of each parameter on ultimate tensile strength (Taguchi).

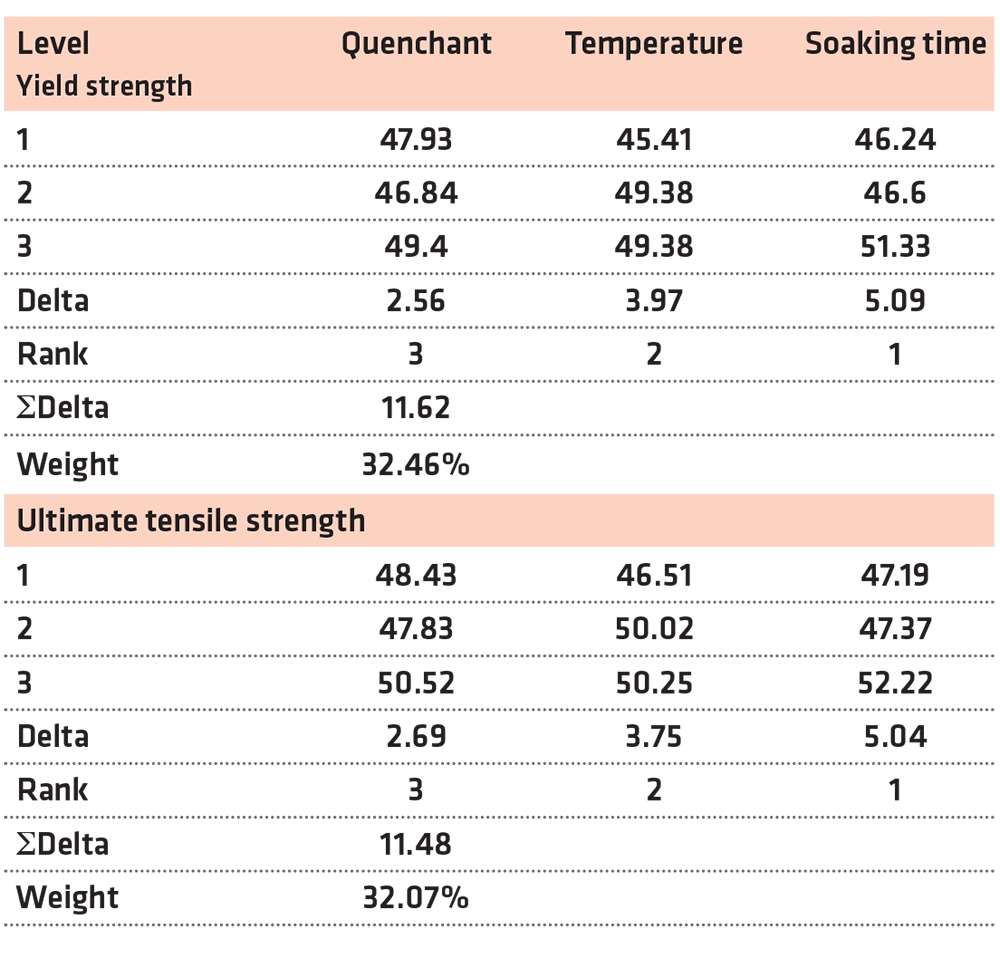
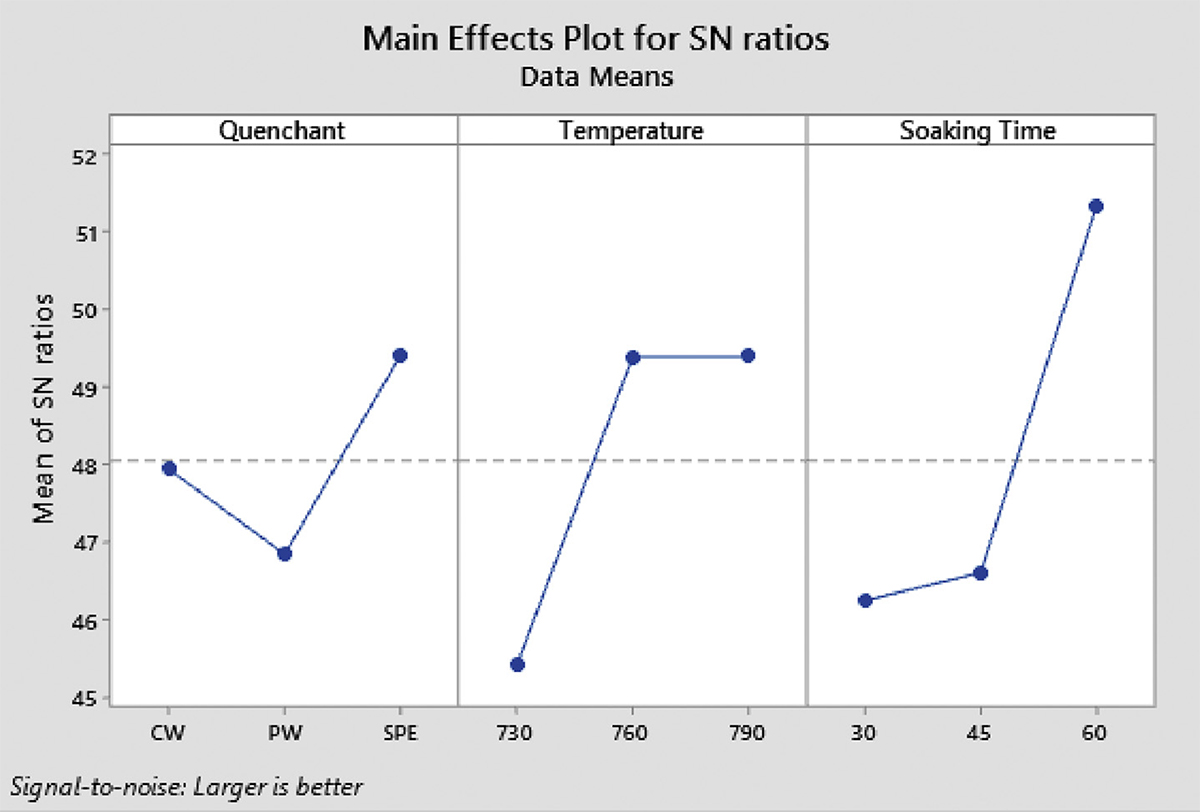
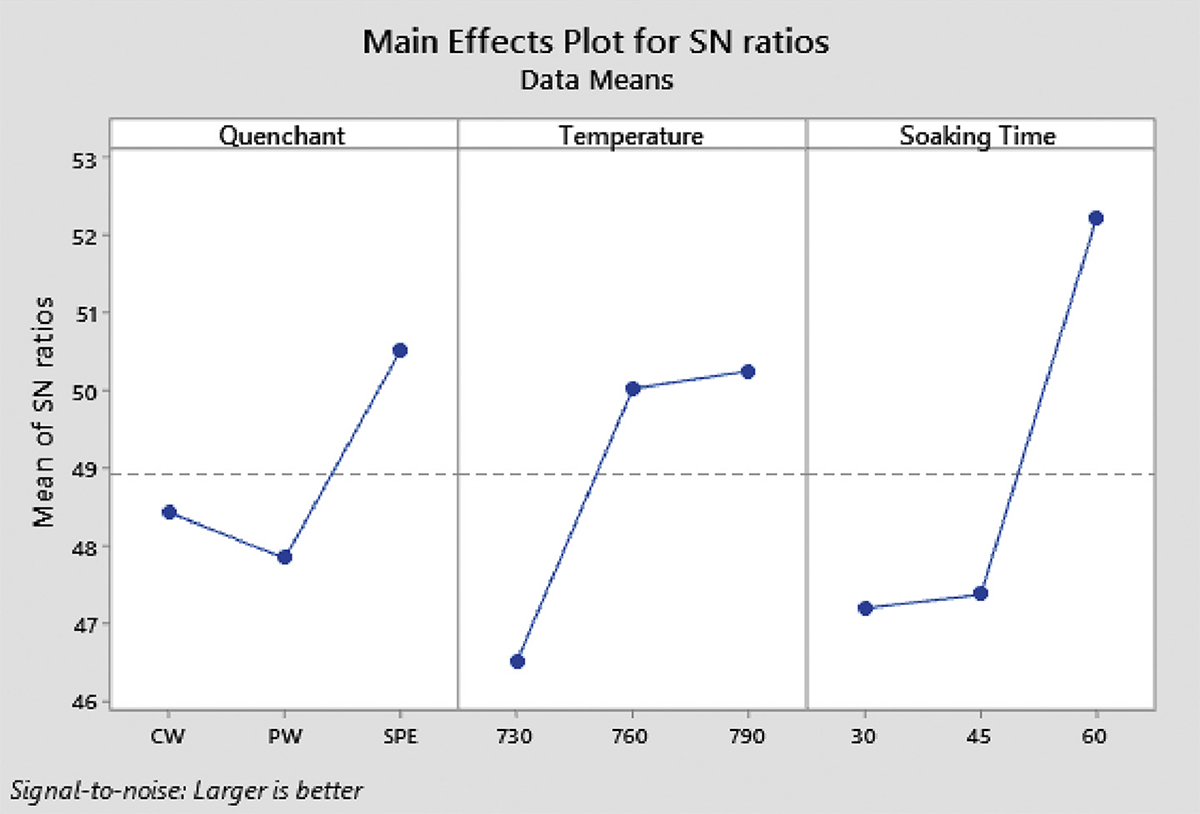
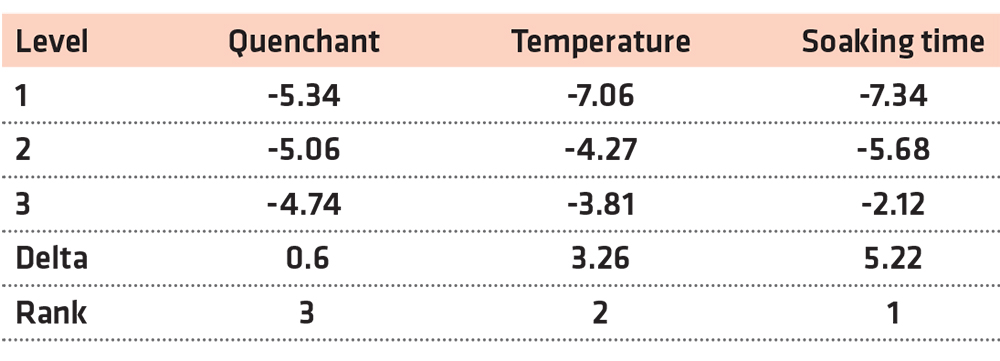
It was stated that the usage of SPE would assist in improving the strength of the MCS. Oil gives better strength compared to water-based quenchants (Adeleke et al., 2018; Vivek et al., 2014; Odusote et al., 2012); hence, for utilization in areas where strength and ductility are important, SPE should be used. The ANOVA results in Table 7 show that soaking time has the largest influence on the YS and UTS of the heat-treated MCS. A similar trend was observed with the contribution ratios in Figure 5, where soaking time has the highest values of 62.46 and 66.76% for the YS and UTS, respectively. Therefore, based on the contribution ratio, the important order of the process parameters on the YS of the heat-treated MCS was Soaking time > Temperature > Quenchant. For all the three target functions (hardness, YS, and UTS), the quenchant was less influential in determining the manner of behavior of the heat-treated medium carbon steel when compared with other parameters such as temperature and soaking time. An increase in soaking time yielded an increase in tensile strength. This agrees with the study of Valdes-Tabernero et al. (2019). The study reported the influence of soaking time on the heat-treatment process of MCS. The Taguchi analysis and ANOVA method used in this study also ranked the soaking time as the most influential factor, followed by the temperature, while the quenchant was ranked least. The ranking order of both methods was the same, which is a means of confirming the reliability of their use as optimization tool (Canbolat et al., 2019; Celik et al., 2018; Chamoli et al., 2016).

Table 7: ANOVA results of the effect of process parameters on the yield and ultimate tensile strengths of MCS.
Figure 5: % contribution of each process parameter on the yield and ultimate tensile strengths of MCS (ANOVA).
3.1.3 Confirmation test

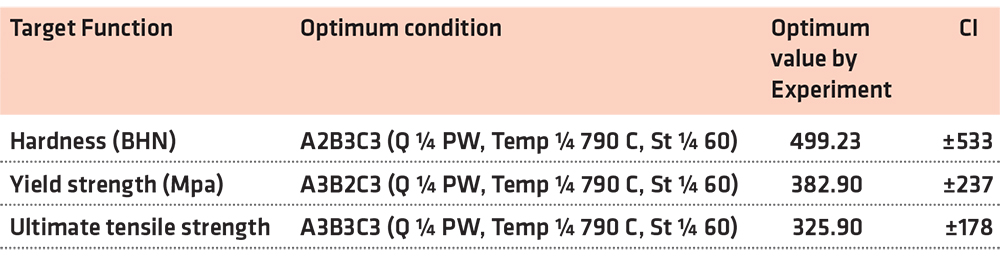
This study conducts a confirmatory check to accurately determine the correct optimization of the process. The obtained result was conducted to check if the values are within the confidence interval (CI). CI was estimated using Equation 6. F0.05,1,2 = 18.51 (F-table),
VeH = 13,813 (Table 4), VeYS = 2,728 (Table 8), and VeUTS = 1,534
(Table 8), R = 3, N = 9, Tdof = 6 and neff 1.2857 (Equation 7). Confirmation experiments were conducted based on the established optimum conditions for each target function and the result is presented in Table 8. The computed values of CI in Table 8 show that experimental optimum values for each process parameter are within an acceptable limit.

Table 8: Experimental values obtained for each target function based on optimum conditions.
3.1.4 Grey relational analysis (GRA)

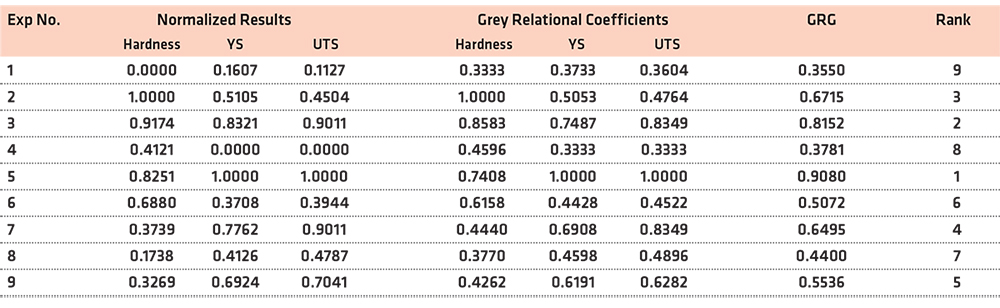
The optimum working conditions obtained from Table 8 are not the same for hardness, YS, and UTS.

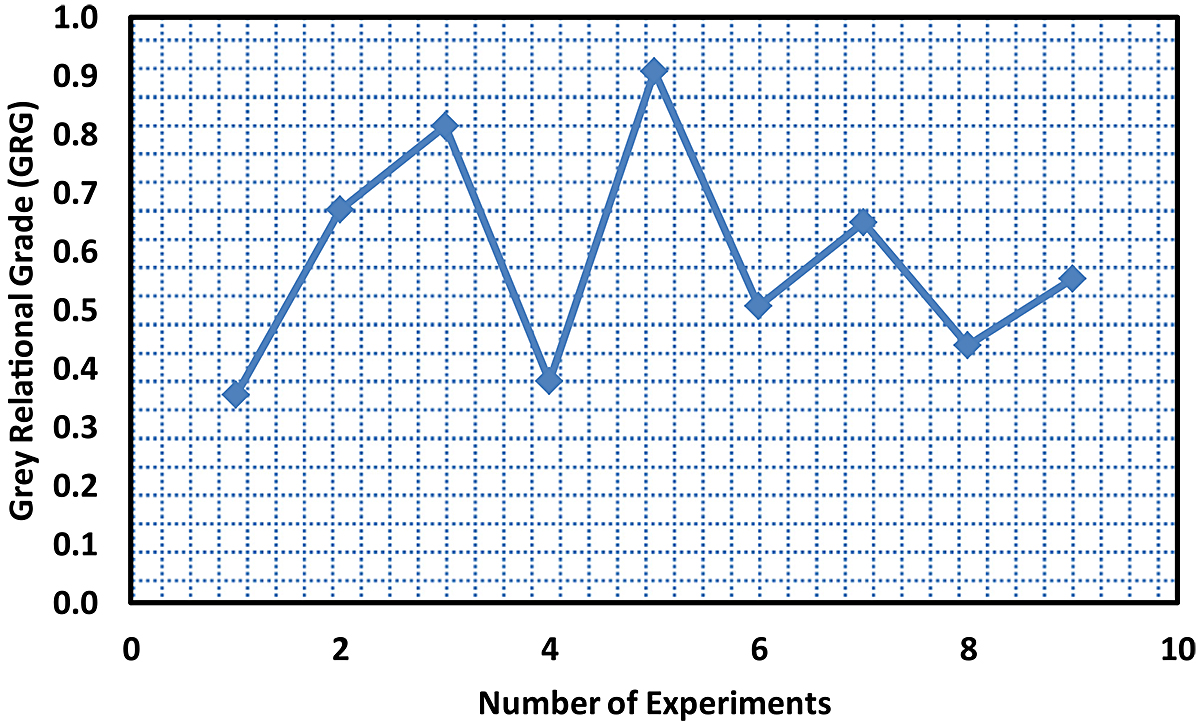
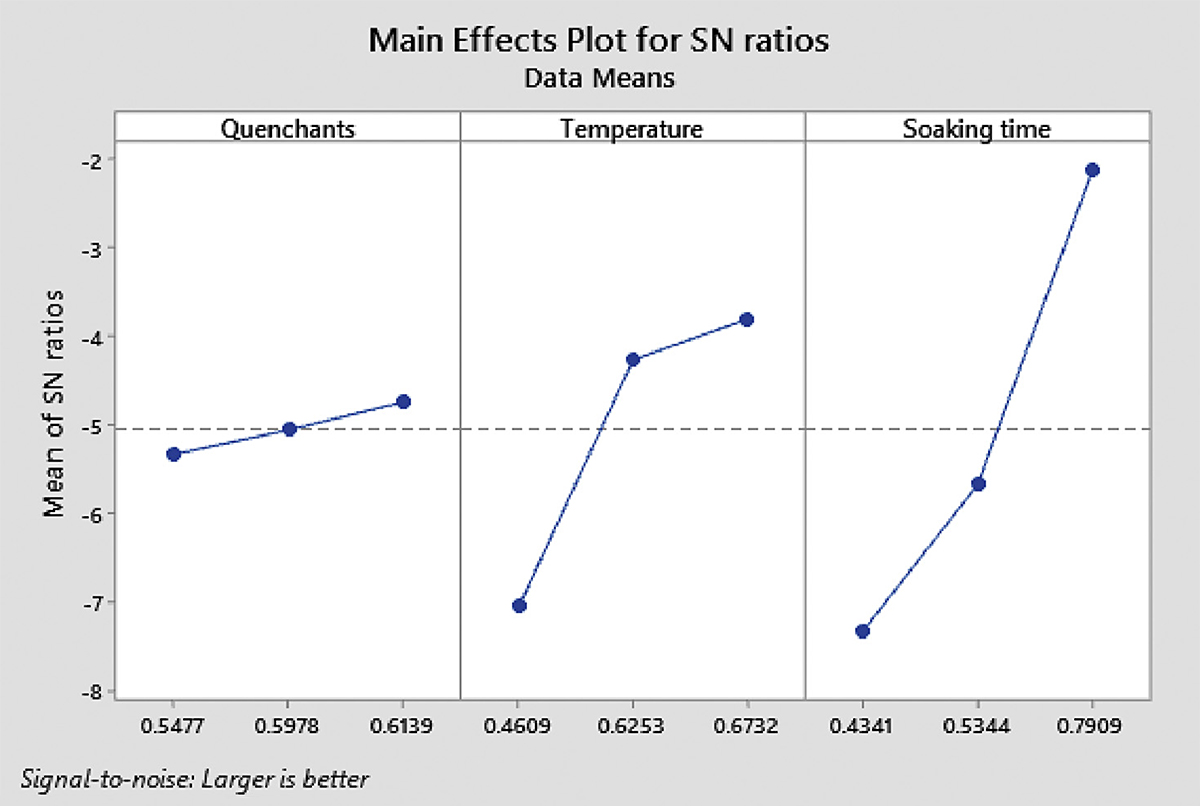
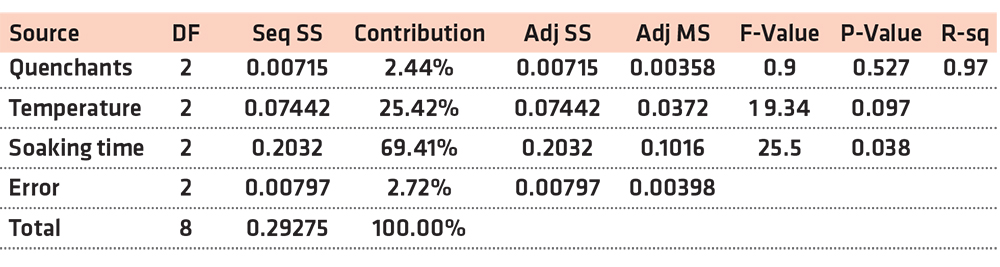
Hence, the multi-objective technique is required to complement the Taguchi method used. GRA method was adopted to reduce the three target functions (maximization of the hardness, YS, and UTS) of MCS into a single objective function (known as multiple performance characteristics, MPC). Using Equations 8, 9, 10, and 11, the result of the normalized response, grey relational coefficients (GRC), grey relational grade (GRG), and ranks were determined and presented in Table 9. The variation of the GRG is shown in Figure 6. According to Kuo et al. (2011), an experiment that has the highest GRG among all the experiments gives the maximum MPC. In this study, experiment 5 gave the maximum MPC. The response was generated, as shown in Table 10, for the GRG to estimate the ranking of the importance of each parameter. Accordingly, the importance orders were ranked as Soaking time > Temperature > Quenchant (Table 10). Figure 7 shows the main effect of each parameter on the MPC of the heat-treated MCS. The level three of each of the process parameters (A3B3C3) gave the optimum condition for multiple characteristics of MCS. ANOVA method was used to evaluate the results of GRG and the % contribution of each parameter, as displayed in Table 11. ANOVA method indicates the soaking time and temperature were the two parameters with the highest effect on MPC with a % contribution of 69.41% and 25.42%, respectively (Table 11). The ranking order is Soaking time > Temperature > Quenchant. These results are consistent with the responses in Table 10 for the grey relational grade.

 

Table 9: Normalized results, grey relational coefficients, grey relational grade, and rank.
Figure 6: GRG for the maximum performance characteristic.
Table 10: Response for GRG.
Figure 7: Main effect for S/N ratios of each parameter on the multiple performance characteristics.
Table 11: ANOVA for Grey relational grade.

4 Conclusion

In the present study, the combination of the Taguchi method and the Grey relational analysis has been used to determine the optimal heat-treatment process parameters required to improve the mechanical properties of medium carbon steel. The heat-treatment parameters such as temperature, soaking time, and quenchant used have been used to analyze the effects on the hardness, yield strength, and the ultimate tensile strength. The experimental results were evaluated and validated by the ANOVA method. It can be concluded that:

The optimal conditions for maximizing hardness, yield strength, and ultimate tensile strength were obtained with the combination found to be A2B3C3 [quenchant (PW), temperature (790°C), and soaking time (60 minutes)]; A3B2C3 [quenchant (SPE), temperature (760°C), and soaking time (60 minutes)], and A3B3C3 [quenchant (SPE), temperature (760°C), and soaking time (60 minutes)], respectively.

• The soaking time is the most significant parameter for all three target functions with 31.95% contribution ratio for hardness, 62.46% for yield strength, and 66.76% for ultimate tensile strength.

• The measured values of the responses (hardness, yield strength, and ultimate tensile strength) were within a 95% confidence interval based on the confirmatory test results.

• The Grey relational analysis and Taguchi method confirmed soaking time as the major process parameters having the highest contribution ratios that were above 60% in both cases.

• The results show that the Taguchi method as well as the Grey relational analysis is a reliable method for the maximization of mechanical properties (hardness, yield strength, and ultimate tensile strength) of medium carbon steel quenched in various media.

Future studies could be considered on the effect of the aforementioned process parameters on the properties and performance of MCS such as corrosion resistance, wear resistance, machinability, and so on.

Author contribution statement

Agboola, O.O. and Ikubanni, P.P.: Conceived and designed the experiments, performed the experiments, analyzed and interpreted the data, wrote the paper. Adeleke, A.A.: Conceived and designed the experiments; performed the experiments, analyzed and interpreted the data. Adediran, A.A., Adesina, O.S., Aliyu, S. J., and Olabamiji, T.S: Conceived and designed the experiments; performed the experiments, contributed reagents, materials, analysis tools or data.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Acknowledgements

The authors appreciate the management of Landmark University for providing a conducive environment for carrying out this research. 

References

  1. Acir, A., Canli, M.E., Ata, I., Cakiroglu, R., 2017. Parametric optimization of energy and exergy analyses of a novel solar air heater with grey relational analysis. Appl. Therm. Eng. 122, 330–338.
  2. Adekunle, A.S., Adebiyi, K.,A., Durowoju, M.O., 2013. Impact of quench severity and hardness on AISI 4137 Using Eco-friendly Quenchant as industrial heat treatment. J. Mech. Eng. Sci. 4, 409–417.
  3. Adeleke, A.A., Ikubanni, P.P., Adediran, A.A., Agboola, O.O., Olabamiji, T.S., Ogunsola, O.J., Ibeawuchi, C., 2018. Tensile strength and microstructural behaviour of medium carbon steel quenched in some selected media. Int. J. Civ. Eng. Technol. 9 (10), 2148–2156.
  4. Adeleke, A.A., Ikubanni, P.P., Orhadahwe, T.A., Aweda, J.O., Odusote, J.K., Agboola, O.O., 2019. Microstructural assessment of AISI 1021 steel under rapid cyclic heat treatment process. Results Eng. 4, 100044, 1–4.
  5. Ahaneku, I.E., Kamal, A.R., Ogunjirin, O.A., 2012. Effects of heat treatment on the properties of mild steel using different quenchants. Front. Sci. 2 (6), 153–158.
  6. Arslanoglu, N., Yigit, A., 2017. Investigation of efficient parameters on optimum insulation thickness based on theoretical-Taguchi combined method. Environ. Prog. Sustain. Energy 36, 1824–1831.
  7. Asilturk, I., Akkus, H., 2011. Determining the effect of cutting parameters on surface roughness in hard turning using the Taguchi method. Measurement 44, 1697–1704.
  8. ASTM E8/E8M-16ae1, 2016. Standard Test Methods for Tension Testing of Metallic Materials. ASTM International, West Conshohocken, PA. www.astm.org.
  9. ASTM E10-18, 2018. Standard Test Method for Brinell Hardness of Metallic Materials. ASTM International, West Conshohocken, PA. www.astm.org.
  10. Bao, Z., Yang, F., Wu, Z., Nyamsi, S.N., Zhang, Z., 2013. Optimal design of metal hydride reactors based on CFD-Taguchi combined method. Energy Convers. Manag. 65, 322–330.
  11. Canbolat, A.S., Bademlioglu, A.H., Arslanoglu, N., Kaynakli, O., 2019. Performance optimization of absorption refrigeration systems using Taguchi, ANOVA and Grey Relational Analysis methods. J. Clean. Prod. 229, 874–885.
  12. Celik, N., Pusat, G., Turgut, E., 2018. Application of Taguchi method and grey relational analysis on a turbulated heat exchanger. Int. J. Therm. Sci. 124, 85–97.
  13. Chamoli, S., Yu, P., Kumar, A., 2016. Multi-response optimization of geometric and flow parameters in a heat exchanger tube with perforated disk inserts by Taguchi grey relational analysis. Appl. Therm. Eng. 103, 1339–1350.
  14. Dvivedi, A., Kumar, P., 2007. Surface quality evaluation in ultrasonic drilling through the Taguchi technique. Int. J. Adv. Manuf. Technol. 34, 131–140.
  15. Gunes, S., Manay, E., Senyigit, E., Ozceyhan, V., 2011. A Taguchi approach for optimization of design parameters in a tube with coiled wire inserts. Appl. Therm. Eng. 31, 2568–2577.
  16. Gupta, A., Singh, H., Aggarwal, A., 2011. Taguchi-fuzzy multi output optimization (MOO) in high speed CNC turning of AISI P-20 tool steel. Expert Syst. Appl. 38, 6822–6828.
  17. Hu, Y., Yang, J., Wang, J., Wang, Q., 2018. Investigation of hydrodynamic and heat transfer performances ingrille-sphere composite pebble beds with DEM-CFD-Taguchi method. Energy 155, 909–920.
  18. Hussein, A. Kh., Abbas, L.K., Hasan, W.N., 2018. Optimization of heat treatment parameters for the tensile properties of medium carbon steel. Eng. Technol. J. 36 (10), 1091–1099.
  19. Ikubanni, P.P., Adediran, A.A., Adeleke, A.A., Ajao, K.R., Agboola, O.O., 2017. Mechanical properties improvement evaluation of medium carbon steel quenched in different media. Int. J. Eng. Res. Afr. 32, 1–10.
  20. Ikubanni, P.P., Agboola, O.O., Adediran, A.A., Adeleke, A.A., Ogunsemi, B.T., Olabamiji, T.S., Uguru-Okorie, D.C., Osueke, C.O., 2018. Experimental data on mechanical properties evaluation of Medium Carbon Steel quenched in different waste media. Data in Brief 20, 1224–1228.
  21. Jun, S.I., McKnight, T.E., Simpson, M.L., Rack, P.D., 2005. A statistical parameter study of Indium tin oxide thin films deposited by radio-frequency sputtering. Thin Solid Films 476, 59–64.
  22. Kumar, V., Singh, H., 2019. Optimization of rotary ultrasonic drilling of optical glass using Taguchi method and utility approach. Eng. Sci. Technol. Int. J. 22 (3), 956–965.
  23. Kuo, C.F.J., Su, T.L., Jhang, P.R., Huang, C.Y., Chiu, C.H., 2011. Using the Taguchi method and grey relational analysis to optimize the flat-plate collector process with multiple quality characteristics in solar energy collector manufacturing. Energy 36, 3554–3562.
  24. Liu, W.L., Hsieh, S.H., Chen, W.J., Wei, P.I., Lee, J.H., 2009. Synthesis of the CuInSe2 thin film for solar cells using the electro deposition technique and Taguchi method. Int. J. Miner. Metall Mater. 6, 101–107.
  25. Mandal, N., Doloi, B., Mondal, B., Das, R., 2011. Optimization of flank wear using Zirconia Toughened Alumina (ZTA) cutting tool: Taguchi method and Regression analysis. Measurement 44, 2149–2155.
  26. Meral, G., Sarıkaya, M., Mia, M., Dilipak, H., S¸ eker, U., Gupta, M.K., 2019. Multi-objective optimization of surface roughness, thrust force, and torque produced by novel drill geometries using Taguchi-based GRA. Int. J. Adv. Manuf. Technol. 101 (5-8), 1595–1610.
  27. Muthuramalingam, T., Ramamurthy, A., Khaja, M., Mohammed, A., Sundar, R., Osama, A., 2020. Enhancing the surface quality of micro Titanium Alloy specimen in WEDM process by adopting TGRA-based optimization. Materials 13 (6), 1440.
  28. Naqiuddin, N.H., Saw, L.H., Yew, M.C., Yusof, F., Poon, H.M., Cai, Z., Thiam, H.S., 2018. Numerical investigation for optimizing segmented micro-channel heat sink by Taguchi-Grey method. Appl. Energy 222, 437–450.
  29. Ndaliman, M., 2006. An Assessment of Mechanical properties of MCS under different quenching media. Assumpt. Univ. J. Technol. 10, 100–104.
  30. Nguyen, H.P., Banh, T.L., Khan, A.M., Tran, D.Q., Pham, V.D., Muthuramalingam, T., Nguyen, D.T., 2020. Application of TGRA-based Optimisation for machinability of high-Chromium tool steel in the EDM process. Arabian J. Sci. Eng. in press.
  31. Odusote, J.K., Ajiboye, T.K., Rabiu, A.B., 2012. Evaluation of mechanical properties of medium carbon steel quenched in water and oil. J. Miner. Mater. Char. Eng. 11, 859.
  32. Palanikumar, K., 2011. Experimental investigation and optimization in drilling of GFRP composites. Measurement 44, 2138–2148.
  33. Sarıkaya, M., Güllü, A., 2014. Taguchi design and response surface methodology based analysis of machining parameters in CNC turning under MQL. J. Clean. Prod. 65, 604–616.
  34. Sarıkaya, M., Yılmaz, V., Dilipak, H., 2016. Modeling and multi-response optimization of milling characteristics based on Taguchi and gray relational analysis. Proc. IME B J. Eng. Manufact. 230 (6), 1049–1065.
  35. Singh, S., Singh, D., Sachan, K., Arya, A., 2013. Effect of soaking time and applied load on wear rate behaviour of carburized mild steel. IOSR J. Eng. 3 (2), 10–19.
  36. Sreeja, V., Dinesh, P., Patil, S.B., 2016. Study of mechanical properties of steel quenched in a blend of biodegradable oils with quench Accelerators. Int. J. Latest Technol. Eng. Manag. Appl. Sci. 5 (5), 20–25.
  37. Taguchi, G., 1987. Taguchi Techniques for Quality Engineering. Quality Resources, New York.
  38. Taguchi, G., Konishi, S., 1987. Orthogonal Arrays and Linear Graphs: Tools for Quality Engineering. American Supplier Institute, Dearborn, Michigan USA.
  39. Tosun, N., 2006. Determination of optimum parameters for multi-performance characteristics in drilling by using grey relational analysis. Int. J. Adv. Manuf. Technol. 28, 450–455. 
  40. Turgay, K., 2014. Optimization of surface roughness and flank wear using the Taguchi method in milling of Hadfield steel with PVD and CVD coated inserts. Measurement 50, 19–28.
  41. Turgut, E., Cakmak, G., Yildiz, C., 2012. Optimization of the concentric heat exchanger with injector turbulators by Taguchi method. Energy Convers. Manag. 53, 268–275.
  42. Valdes-Tabernero, M.A., Celada-Casero, C., Sabirov, I., Kumar, A., Petrov, R.H., 2019. The effect of heating rate and soaking time on microstructure of an advanced high strength steel. Mater. Char. 155, 109822, 2019.
  43. Vivek, T., Adarsh, P., Zuber, M., Chardreshekar, I.B., 2014. Prediction of quench severity of various quenching media based on hardness and microstructure studies. Int. J. Innovat. Res. Adv. Eng. 1 (3), 20–26.

© 2020 Published by Elsevier Ltd. (https://doi.org/10.1016/j.heliyon.2020.e04444) This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/). This article has been edited to conform to the style of Thermal Processing magazine.

SHARE
Previous articleCarburizing clean with Method 4
Next articleThe subtleties of induction processing
O.O. Agboola
O.O. Agboola is with the Department of Mechanical Engineering, Landmark University, Omu-Aran, Nigeria.
P.P. Ikubanni
P.P. Ikubanni is with the Department of Mechanical Engineering, Landmark University, Omu-Aran, Nigeria.
A.A. Adeleke
A.A. Adeleke is with the Department of Mechanical Engineering, Landmark University, Omu-Aran, Nigeria.
A.A. Adediran
A.A. Adediran is with the Department of Mechanical Engineering, Landmark University, Omu-Aran, Nigeria.
O.S. Adesina
O.S. Adesina is with the Department of Mechanical Engineering, Landmark University, Omu-Aran, Nigeria.
S.J. Aliyu
S.J. Aliyu is with the Department of Mechanical Engineering, Landmark University, Omu-Aran, Nigeria.
T.S. Olabamiji
T.S. Olabamiji is with the Department of Mechanical Engineering, Landmark University, Omu-Aran, Nigeria.

RELATED ARTICLESMORE FROM AUTHOR