In this column, I will discuss the thermal expansion of oil. This information is primarily important for initial fills of a quench tank.
Introduction
Oil, when heated, expands. This is important for the initial fill of the quench tank, as well as determining the expansion of the oil during quenching. The goal is to provide adequate freeboard so that the oil does not overflow the quench tank and potentially cause a fire or explosion, or a large spill.
Often, a furnace manufacturer will have already determined the maximum volume of the oil allowable during quenching. However, this volume is calculated at the temperature of use, not ambient temperature for filling. If the quench tank is initially filled to the maximum level, and the oil is heated to the operating temperature, the oil will expand and potentially cause a fire or explosion hazard. Therefore, it is necessary to know how much oil to put in the tank, so that when the oil is heated, it will expand to the proper level.
Calculation
The thermal coefficient of expansion is dependent on the dynamic viscosity of the fluid. The unit of dynamic viscosity in CGS units is the poise, named after Jean Le´onard Marie Poiseuille. It is commonly expressed as centipoise (cP). Chu and Cameron [1] established a correlation for the thermal expansion of mineral oils over a wide range of dynamic viscosities and is shown in Figure 1.
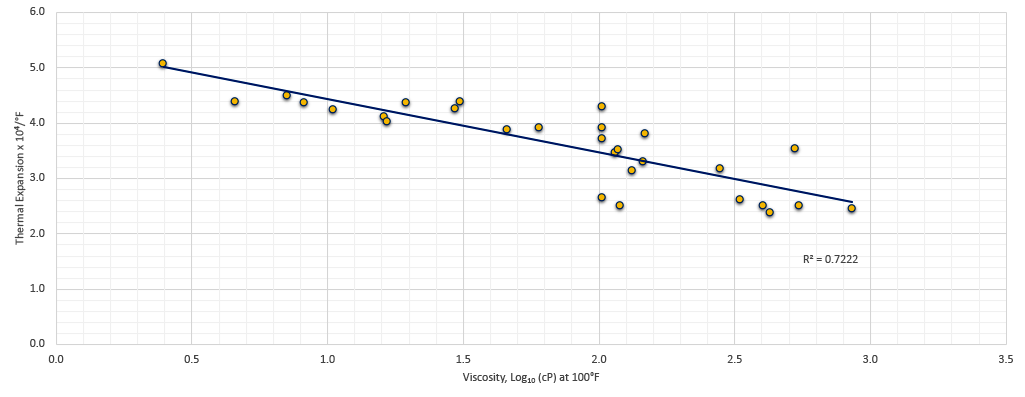
While the scatter of the measurements was large (R2 = 0.772), a linear regression of the data resulted in the following equation (in units of °F-1):
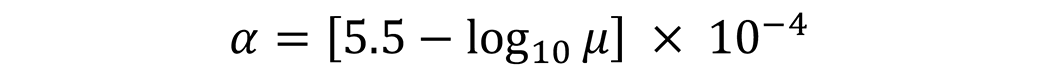Where α is the thermal coefficient of expansion, μ is the dynamic viscosity oil at 100°F in centipoise. For a typical quench oil with a kinematic viscosity of 22 cSt, the thermal expansion coefficient is 0.0004223 °F-1. This is converted to metric units by multiplying by 1.8 to get the units in °C-1.
The commonly found kinematic viscosity (cSt) found in most technical data sheets to dynamic viscosity used in this equation can be found by multiplying the specific gravity by the kinematic viscosity:
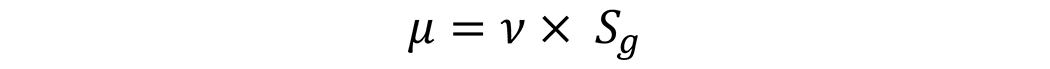Where ν is the kinematic viscosity in centistokes, and Sg is the specific gravity of the product. Typical values for different products over a range of viscosities are shown in Table 1.
The thermal expansion of mineral oil is calculated from the following equation:
Simplifying:
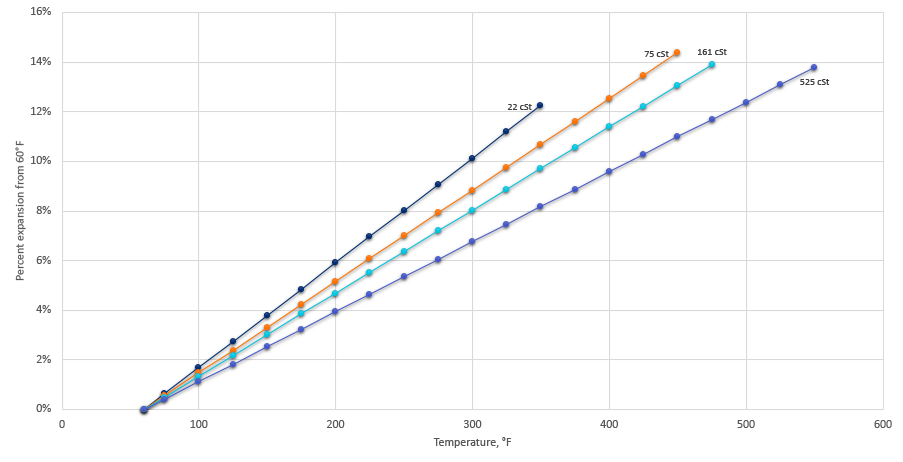
Where Vf is the final volume, α is the thermal coefficient, V0 is the initial volume, Tf is the final temperature, and T0 is the initial temperature. The thermal expansion of the products shown in Table 1, up to their flash point, is shown in Figure 2. For most products, the expansion is on the order of 15 percent when approaching the flash point of the oil.
Example Calculation
In this instance, I have a new installation of a furnace, nominally designed for 3,000 gallons of oil when up to the operating temperature of 180°F. The oil is a typical fast, cold oil with a viscosity of 26.1cSt at 100°F, and a specific gravity of 0.86. The ambient temperature of the shop is 75°F. I want to know how much to buy for the initial fill.
The first thing to determine is the dynamic viscosity in cP. Since the kinematic viscosity of the product is 26.1 cSt, and the specific gravity is 0.86, the dynamic viscosity in cP is 26.1 cSt * 0.86 = 22.44 cP. Substituting this value into the following equation, the coefficient of thermal expansion is determined:
Or a value of α = 4.083 x 10-4/°F.
Since the desired volume of oil at the operating temperature is 3,000 gallons, this is the final volume, Vf. Rearranging the volume equation
To yield the initial volume, results in:
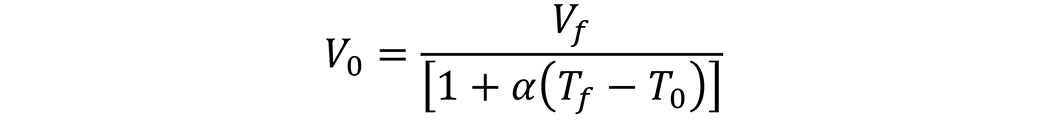Substituting the known values (final volume of 3,000 gallons, initial temperature 75°F, and operating temperature of 180°F):
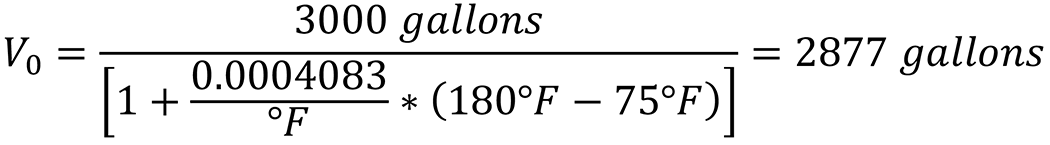For my quench tank, I would need to buy 2,877 gallons of quench oil to fill my 3,000-gallon quench tank at the operating temperature of 180°F. Realistically, 3,000 gallons would probably be bought to compensate for drag-out, but the quench tank would initially be filled with 2,877 gallons that would expand to 3,000 gallons as the quench tank was heated to the operating temperature.
Conclusions
In this short article, a method has been shown to determine the thermal expansion of an oil once the specific gravity and kinematic viscosity are known. This allows a quench tank to be filled and brought up to operating temperature without fear of overflowing the quench tank.
Should there be any suggestions regarding this column, or suggestions for new columns, please contact the editor or myself.
References
- P. S. Chu and A. Cameron, “Compressibility and Thermal Expansion of Oils,” Journal of the Institute of Petroleum, vol. 49, no. 473, pp. 140-145, May 1963.
