
Age-hardenable alloys, such as some aluminum alloys, maraging steel, and nickel-based alloys, get their strength not from quenching but from the precipitation that occurs during the aging or tempering process. While the types of precipitates are different for each alloy, the mechanism is similar. During aging, alloys come out of the base matrix of the material and combine to form nano-scale precipitates; these precipitates strengthen the material by blocking the path of any dislocations that may form and travel through the grain. The general heat treatment of these materials includes a solution treatment to dissolve any precipitates that have been formed, quenching to maintain the solid-solution matrix, and an aging or tempering step to allow the precipitates to nucleate and grow. Higher temperatures aid in precipitation, but temperatures too high will coarsen the precipitates, reducing their strengthening effect. Modeling this phenomenon can be challenging due to the precipitates having different rates of formation and coarsening at different aging temperatures; the large range of temperature the material undergoes during heat treatment; and the effect these precipitates have on the mechanical properties of the material such as ductility, yield strength, and hardness. An analytical model is needed to predict the microstructural evolution during the solution treatment, quenching, aging, with respect to precipitate formation, growth, and coarsening.
Solution Treatment
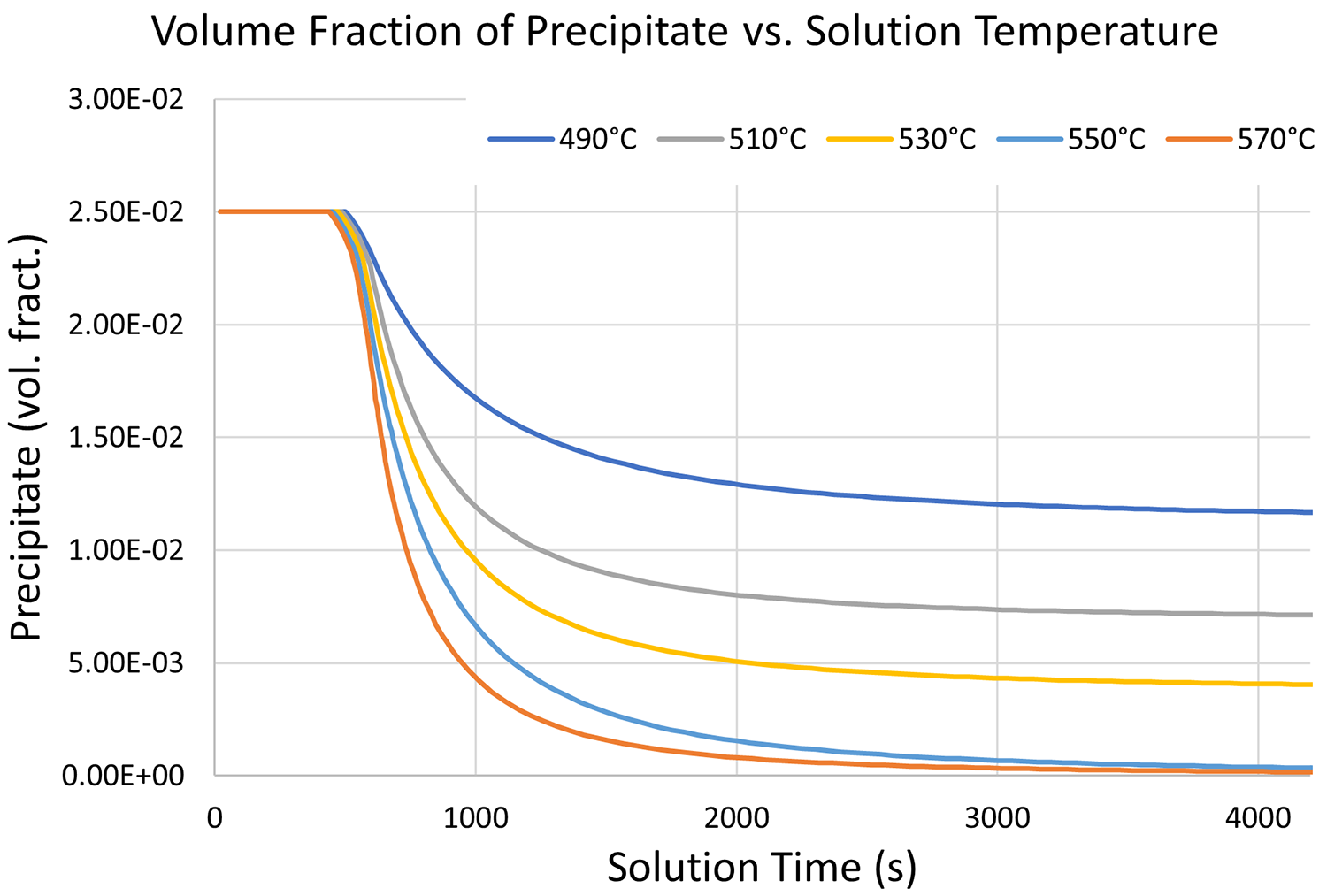
Solution treatment of age-hardenable alloys includes heating the material to a sufficient temperature and holding to decompose and dissolve the precipitates into the matrix. The temperature has a significant effect on the rate and completeness of the solutionizing step, with higher temperatures speeding up the process. However, grain growth at higher temperatures is a concern. As with most heat treatments, a balance point between furnace time and grain size is needed. With modeling, one can predict the time required at temperature to ensure all the precipitates are dissolved, but an accurate material model is required for the kinetics of decomposition. Data for the solution treatment kinetics can be gathered from isothermal holds at an array of solution temperatures and measuring the subsequent hardness, or by in-situ X-ray diffraction techniques. Figure 1 shows the results of the solution treatment model that was developed for 6061 aluminum. The plot shows the volume fraction of precipitates, initially at 2.5 percent, over time at a range of temperatures from 490°C to 570°C. At 490°C, the decomposition of precipitate A is slow and, after an hour hold, over 1 percent of precipitates remains undissolved. In contrast, holds at 550°C and 570°C begin to dissolve the precipitate much faster and the solution treatment is numerically complete after an hour of holding time.
Aging
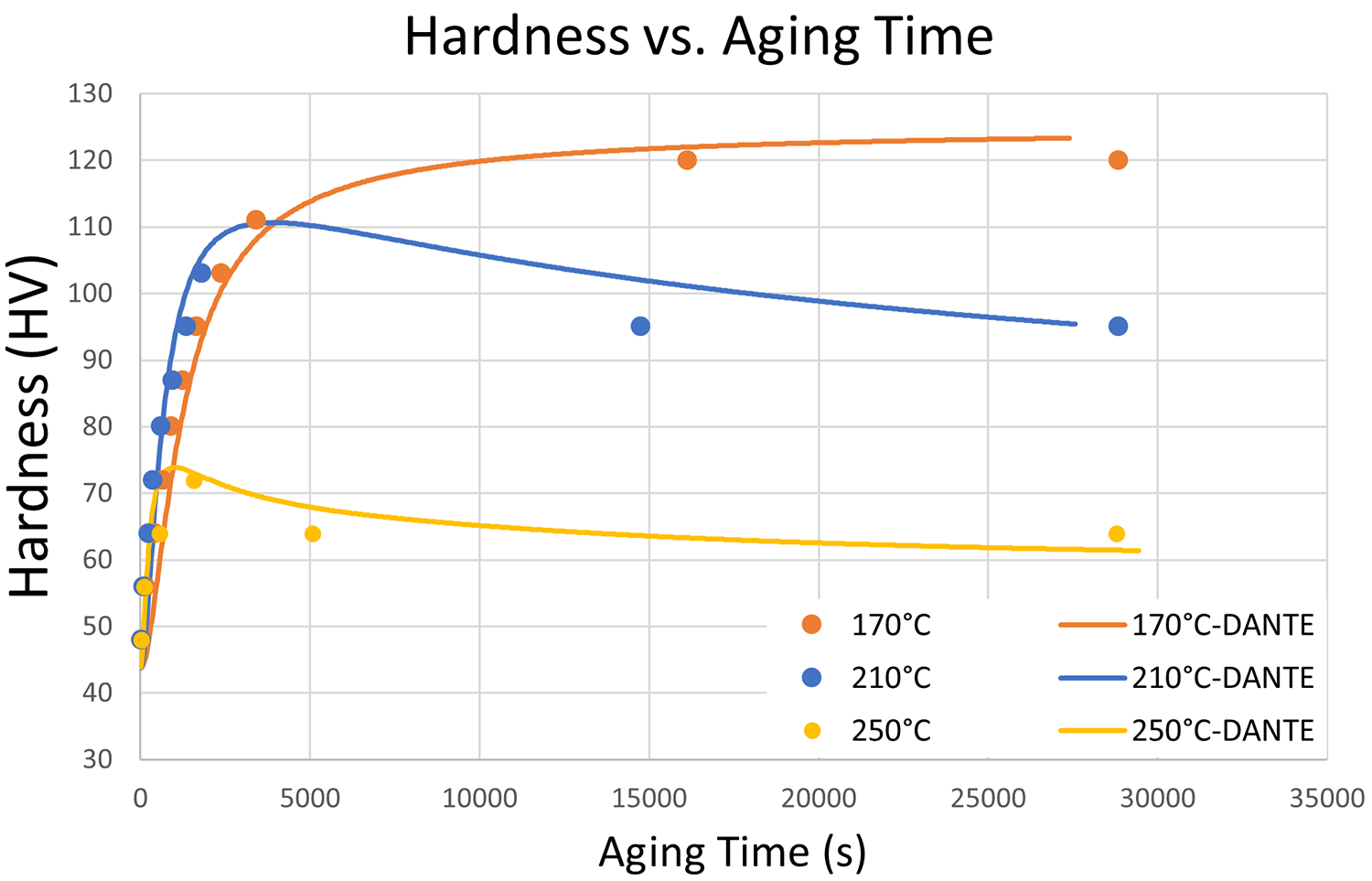
After solution treatment and quenching, age-hardenable alloys are subjected to temperatures below the solution treatment temperature and held for long periods of time to allow the alloys to precipitate and form the main hardening phases. There exists a Goldilocks zone in temperature where the precipitates are allowed to diffuse and combine but not coarsen excessively, which would reduce their hardening potential. For modeling, data is required over a large temperature range as precipitation can occur while the part is transitioning through these temperatures. Figure 2 shows Vickers hardness results versus aging time for three temperatures for 6061, both experimental and simulated. Artificial aging at 170°C provides a slow and steady increase in hardness over time with a peak hardness occurring at the end of the process. At 210°C, peak hardness occurs early in the process and coarsening of the precipitates causes a reduction in hardness over the remainder of the processing time. At 250°C, the coarsening of the precipitates overshadows the formation of precipitates, and the hardness never reaches peak values, illustrating an extremely overaged condition. Typically, aging would not be performed at this temperature due to the rapid coarsening of precipitates. However, it is important to include the kinetics for this temperature, as a bulky part will cool from solution treatment more slowly in the core, often causing this overaged condition before the part ever sees the aging step.
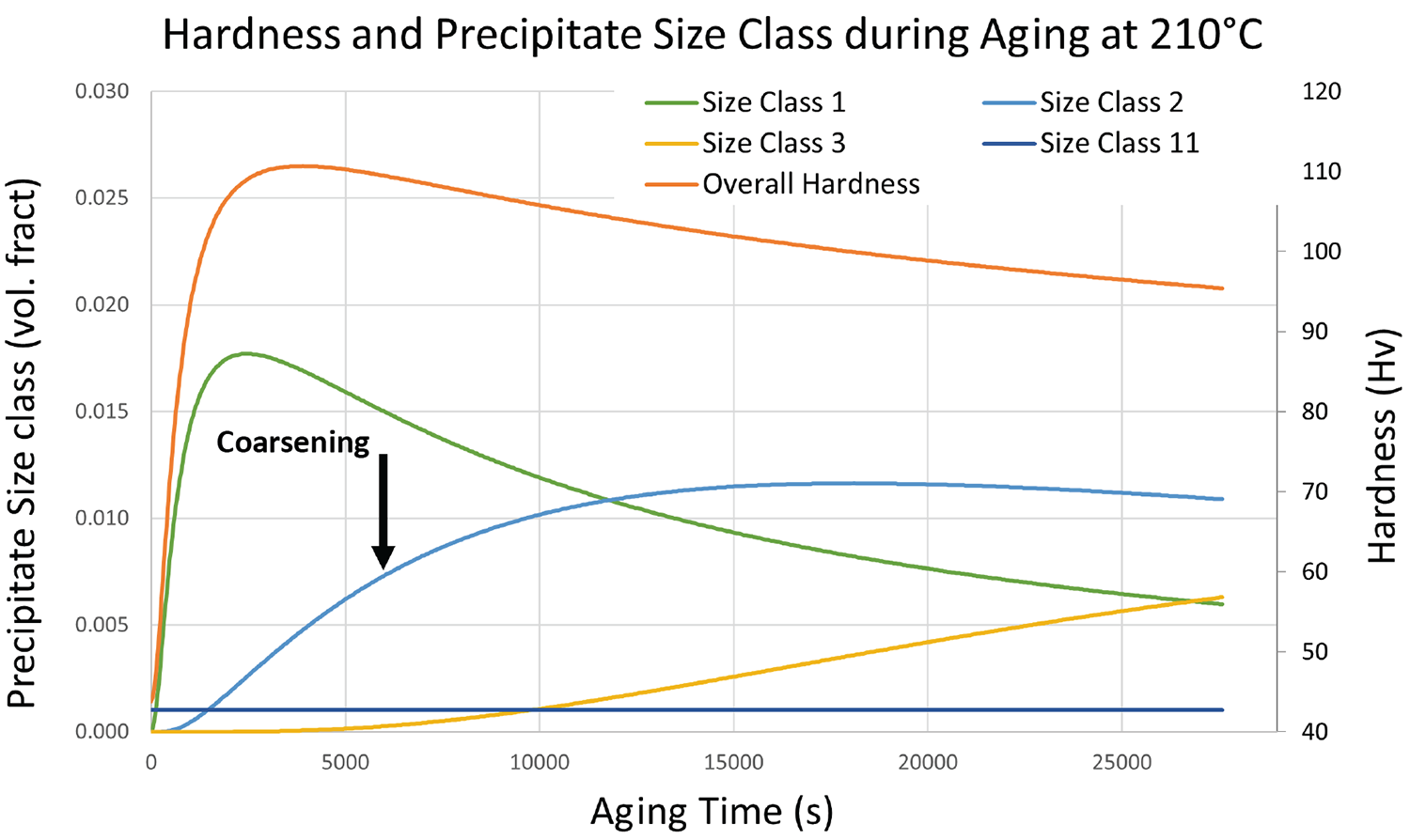
An effective analytical model for age-hardenable materials must track the size of these precipitates through the process of formation, and coarsening. DANTE uses a size class to define the precipitation and coarsening, with 11 different classes the precipitates can evolve through. When precipitates form, they begin as size class one, and if the temperature is high enough or time long enough, they coarsen to size class 2, and so on to size class 11. These size classes are two-fold in that they track the actual size of the precipitates and are used to adjust the mechanical properties in real time during the simulation. Size class 11 precipitates contribute very little to the hardness and subsequent mechanical performance of the alloy. Figure 3 shows the size class evolution and its effect on the hardness of 6061 at 210°C. When the aging starts, we can see the volume fraction of size class 1 precipitates rise with the overall hardness. As size class 1 begins to coarsen to size class 2, the overall hardness begins to decrease, and so on as size class 3 forms.
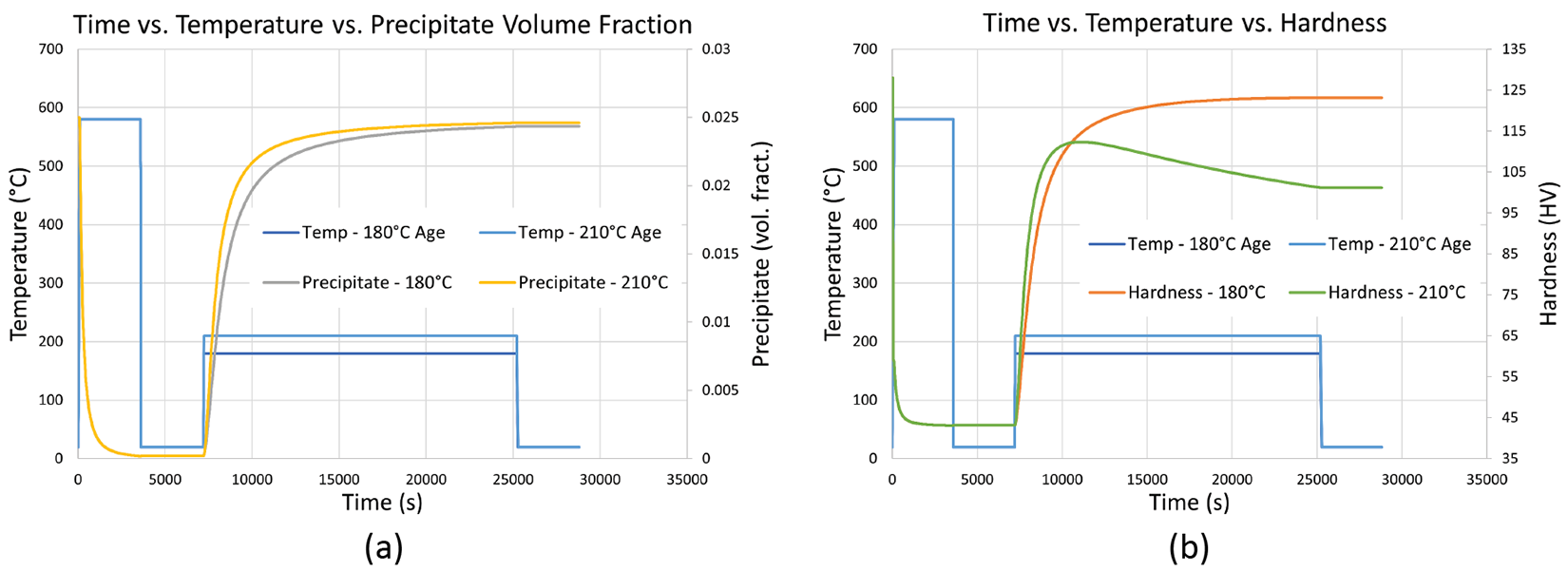
Putting all this work on solution treatment and precipitate nucleation and coarsening together completes the precipitate phase kinetics. Figure 4 shows two time-temperature plots for a simulated solution treatment, quenching, and artificial aging process at 180°C and 210°C. Figure 4(a) shows the volume fraction of precipitates during the process, while Figure 4(b) shows the hardness during the process. Figure 4(a) shows that while the rate of formation of precipitates is faster in the 210°C aging than the 180°C aging, they both end up with about the same volume fraction after aging. Figure 4(b) shows that despite the same volume fraction of precipitates, the hardness is much lower in the 210°C aged simulation due to the coarsening of the precipitates.
Mechanical Model
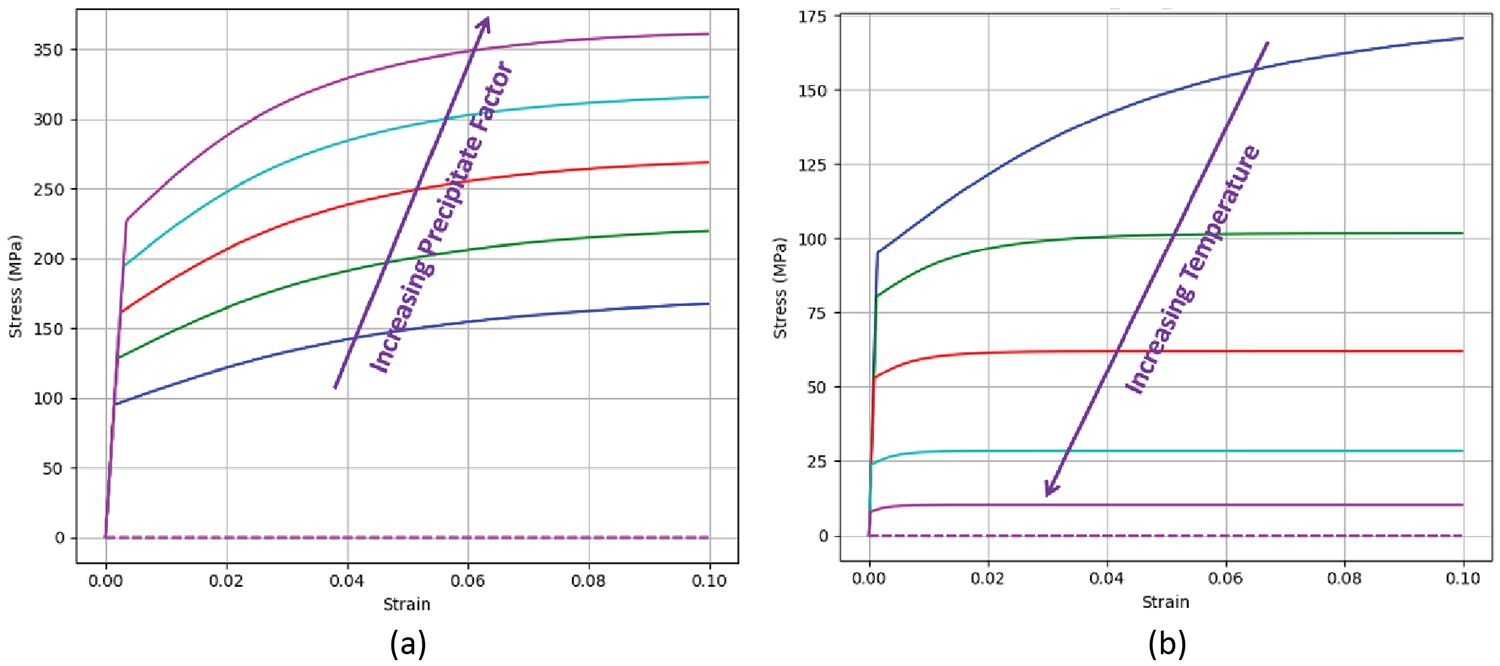
The final piece to modeling age-hardenable materials is the mechanical model to account for the stress/strain response during heat treatment. These parameters are used to simulate the in-process and residual stress states and the distortion from the heat-treatment process. An effective mechanical model must include effects from temperature, strain, strain rate, and precipitates including coarsening. Using the previous work with coarsening and hardness, a factor is used to account for the influence that precipitates have on hardness, and thus mechanical performance. This factor is applied to DANTE’s internal state variable plasticity model, and is used to describe the yield, hardening, and recovery during heat treatment. Figure 5 shows this general stress/strain relationship with increasing precipitate factor (a) and increasing temperature (b). In general, the more contribution the precipitates have to hardness, the higher the yield strength, and as the temperature rises, the yield strength is reduced. Coarsened precipitates will have less of an influence on hardness.
Conclusions
The material models implemented in DANTE successfully showed the capability of modeling the complicated age-hardening process consisting of predicting the microstructural evolution during the solution treatment, quenching, aging, and with respect to precipitate formation, growth, and coarsening. While this work showed examples using 6061 aluminum, the models developed can be used for any age-hardenable alloy, including precipitation hardened stainless steel, maraging steel, and nickel-based alloys.

























