Analysis of Heat Treat Growth on Carburized Ring Gear and Multivariate Regression Model Development

In gear manufacturing and machine assembly, dimensional stability of each component and conformance to print requirements are of critical importance. During processing, dimensional changes associated with each manufacturing step must be consistent and predictable so that the final part size conforms to the print tolerances and assembles properly. Misalignment of the assembled components may cause excessive noise during operation and premature failure of the mating components [1, 2]. Typical industrial ring gear manufacturing includes green (i.e., prior to heat treat) machining that may involve lathing, hobbing, or grinding, followed by a carburizing and hardening heat treatment to enable desired mechanical properties, and finally, hard grinding to ensure dimensional conformance to print [3]. Like most other heat treatments, the carburizing and hardening process is known to introduce dimensional changes and gear distortion [4]. If these size and shape changes can be anticipated and controlled, it is possible to eliminate post–heat treatment machining by designing ring gears that would allow for the heat treat change. Such gear manufacturing would significantly reduce cost and machining-to-assembly time, both of which are critical in a commercial environment and large-scale production.

To establish proper green gear size, a heat treat test lot (HTTL) is generally conducted that involves processing gears through their entire manufacturing path with the addition of high accuracy dimensional measurements before and after heat treatment [3, 4]. Heat treat size change is then calculated for the critical geometrical features, and the desired green gear size is determined based on the final print requirements and observed heat treat growth. HTTLs are typically performed when developing new gears or implementing various design or process modifications on current production gears, such as changes in supplier, case depth, material, and process changes. While HTTL data provide the information needed, they are expensive and time-consuming and may take many weeks to complete. For new gear development, an initial attempt to estimate the desired green size is frequently based on an engineering estimate and historical data for similarly designed gears. As a result, two to three HTTLs are often required to establish the optimal green gear size and may add many months to the process development and validation timeline. Therefore, the ability to predict and account for the gear dimensional changes during heat treat could be of great benefit and yield substantial cost savings.

Several publications have addressed the distortion issues during surface hardening. Bahnsen et al. [5] studied the influence of carburizing case depth, surface carbon, and process temperature on shaft distortion behavior and reported that carburizing case depth has the most dominant effect. Bomas [6] experimentally confirmed that the dimensional changes in carburized samples can be related to the carburized depth-to-wall thickness ratio. Clausen et al. [7] reported that changes in length of the carburized shaft are inversely proportional to the carburized depth-to-radius ratio and total carbon flux. Other researchers [8-10] studied the effect of material hardenability, quench oil temperature, and velocity on flat rings geometry. While all researchers agreed that size and shape changes in the carburized components are multivariate in nature, these studies reported design of experiments (DoE) results on basic simplified geometry parts and are not comprehensive enough to deduce any predictive models for heat treat changes as a function of the key geometrical features and process characteristics.

This development work considered a wide range of ring gear sizes and geometries and was based on the extensive statistical analyses of the HTTL data collected concurrently with large-scale ring gear manufacturing. The main objective was to develop a better tool for predicting heat treat changes during carburizing to help determine the optimal green size based on various gear design features and process parameters. Ultimately, the heat treat growth model would be used to reduce and potentially eliminate the need for the HTTL, thus reducing time and cost associated with ring gear development and validation.

Experimental Protocol

An extensive database was created from the existing HTTL data. The first data set included 10 part numbers (146 gears total) of various gear geometry and green hardness data. Additional historical HTTL data were available that did not contain green hardness measured on gears prior to heat treatment. Thus, a larger database was also populated and consisted of 19 part numbers (314 gears total) with similar data structure, but without green hardness available. From the authors’ previous experience, green hardness — reported in this paper as the diameter of the hardness impression (HBD) — appeared to be an important parameter influencing gear growth during carburizing. Therefore, analyzing both datasets was advantageous, allowing green hardness to be one of the predicting factors, as well as providing a wider range of gear sizes and geometries.

All gears were measured in the metrology lab before and after heat treatment using CMM/PMM measurements with 2-micron accuracy. The gears were carburized in gas-fired pusher-type furnaces to produce a target hardened depth within a 0.6 to 1.2 mm range. The typical carburizing cycle consisted of a boost at 927°C and 1.1 wt.% carbon potential, a diffuse at 850°C and 0.85 wt.% carbon potential, and direct quenching in agitated oil. Carburizing cycle time was adjusted for each part number based on the print-required case depth.

The gears were made of AISI 4120 and AISI 4122 medium-alloy gear steel with slight modifications in Mo and Cr content yielding nominal hardenability ideal diameters (DIs) of 52, 70, and 89 mm. The range of ring gear geometry included:

• OD: 326-900 mm
• Tip diameter: 284-874 mm
• Root diameter: 300-927 mm
• Height: 47-266 mm
• Gear cross-section: 12.4-55.4 mm
• Mid-tooth thickness: 6.3-1.2 mm

Statistical data analyses were performed using Minitab [11]. Input factors included material hardenability, the aforementioned key geometrical characteristics, and case depth (defined as the depth from the part surface to the depth where the material carbon content is 0.35 wt.%) calculated from the heat treat cycle history and finite difference carburizing process modeling. Although heat treat growth was measured on all key geometrical features, the initial model development presented here is focused on modeling heat treat growth of the measurements between pins (MBP), as this determines the ability of the gear to be assembled and fit for application. In the future, similar models will be developed to predict heat treat growth during carburizing and hardening on the rest of the critical geometrical features of the ring gear.

Results and Discussion

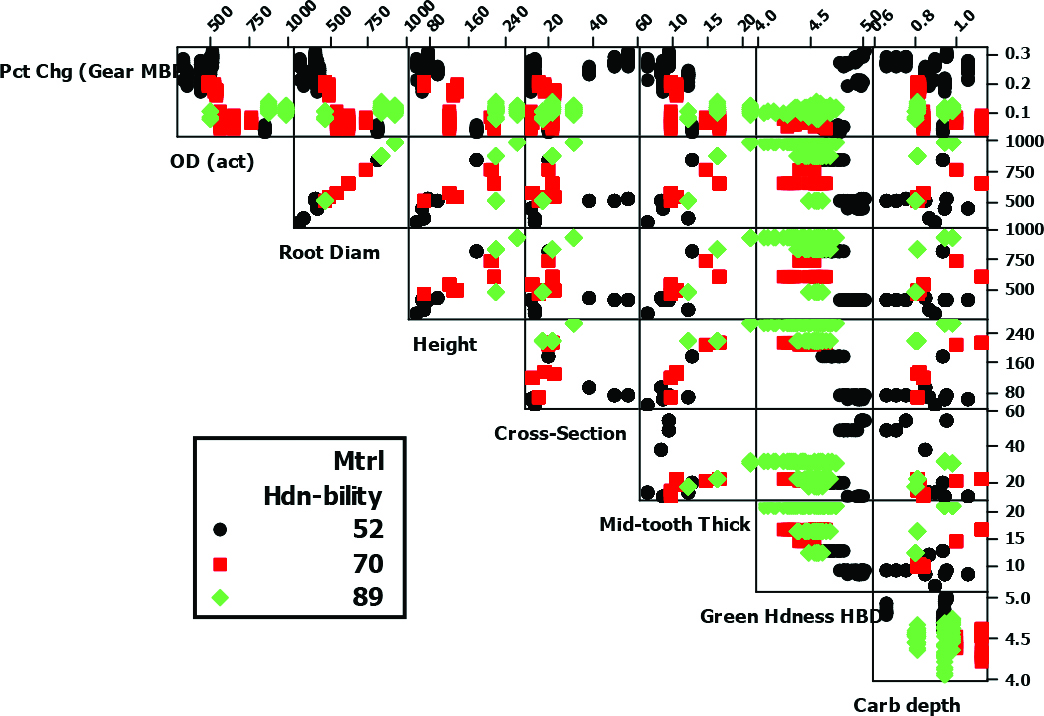
Figure 1 shows the matrix plot for the MBP percent change versus various geometrical characteristics and process parameters. High-level correlation (shown as strong linear trends) of several of the geometrical characteristics reflect similarities of some of the gear designs, e.g., larger OD and tip diameter gears tend to be taller and have greater mid-tooth thickness. Such gears are typically carburized to deeper case depths and tend to be made of a steel grade with greater hardenability. While the trend in MBP percent change is multivariate in nature, it appears to be proportional to gear cross-section and inversely proportional to gear mid-tooth thickness. Ring gears with greater green hardness (softer) tend to grow more, which agrees well with the observations made in the previous studies performed on several ring gear part numbers.

Analysis with green hardness data

Table 1 shows the results of the ANOVA analysis for the dataset with green hardness data. The model with the selected predictors proved to be statistically significant with p-value approaching zero. Of all the factors considered, ring gear tip diameter, material hardenability and height were found to be the most significant in influencing the degree of gear MBP growth. Variance inflation factors (VIF) were analyzed to help identify multi-collinearity, which will influence the regression results and the fitted parameters. Ring gear mid-tooth thickness, tip, and root diameter were found to be highly correlated with the other factors.  As a result, mid-tooth thickness was removed from the model.

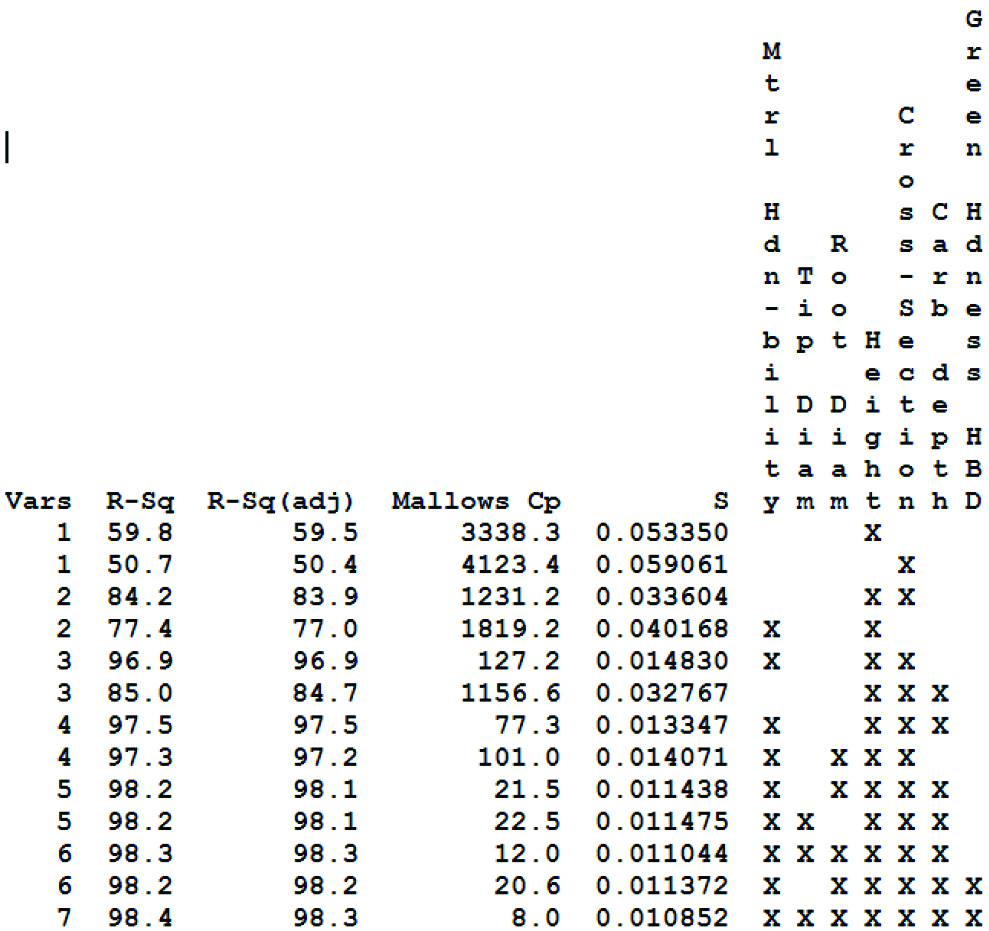
Like in most other multivariate regression systems, the response variable (heat treat growth during gas carburizing and hardening) can be described by using various combinations of the predicting factors. Table 2 and Table 3 show the best subset model results for the gear MBP percent change and the actual MBP growth, expressed in millimeters, as a function of various combinations of the geometrical and process parameters. The same factors were used in each best subset model to assess which response variable correlated better with the measured results.

Gear MBP percent change revealed a higher R² and greater predicting power than the actual gear MBP growth. This can be explained by the “normalizing” effect of MBP percent change, which takes a ratio of the observed heat treat growth to the actual gear size. This is particularly beneficial given the wide range of gear sizes used in this study. As follows from Table 2 and Table 3, just three factors — material hardenability, height, and gear cross-section — explain most of the observed heat treat growth variation. From the principle of parsimony, this model may be considered as the optimal, as it utilizes the minimum number of predicting factors to explain the maximum degree of variation. However, this model reveals a high Mallows’ Cp value, a statistical factor commonly used to help choose between compelling multiple regression models [11]. A Mallows’ Cp value that is close to the number of the predicting factors plus the constant indicates a more optimal model that is relatively precise and unbiased in estimating the true regression coefficients and predicting future responses. Thus, the best subset analysis identified the model that yields 98.3-percent R²_adj and utilizes seven parameters — material hardenability, tip diameter, root diameter, height, cross-section, carb depth, and green hardness — as best able to predict heat treat growth, expressed in terms of gear MBP percent change.

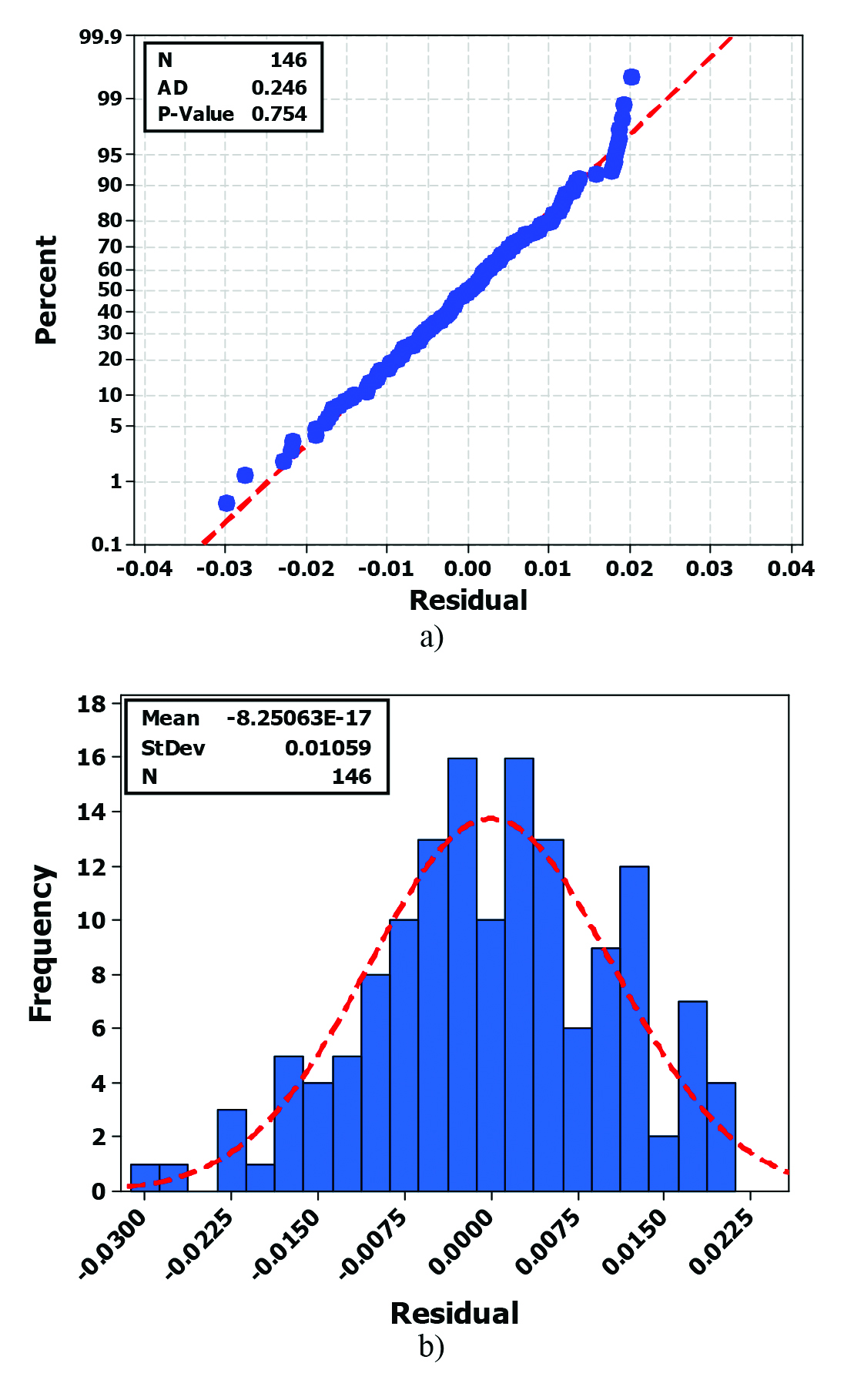
Figure 2 shows the results of the residuals analysis for the best subset model. The normal probability plot (Figure 2-a) with p-value of 0.754 passes the test for normality, though some deviation is observed in the tails. The histogram of the residuals with the fitted normal distribution probability curve (Figure 2-b) shows the spread and confirms some deviation from normality in the tails. These may be resolved as more HTTL data in this ongoing project become available and a larger gear geometry and size range are considered.

Analysis without green hardness data

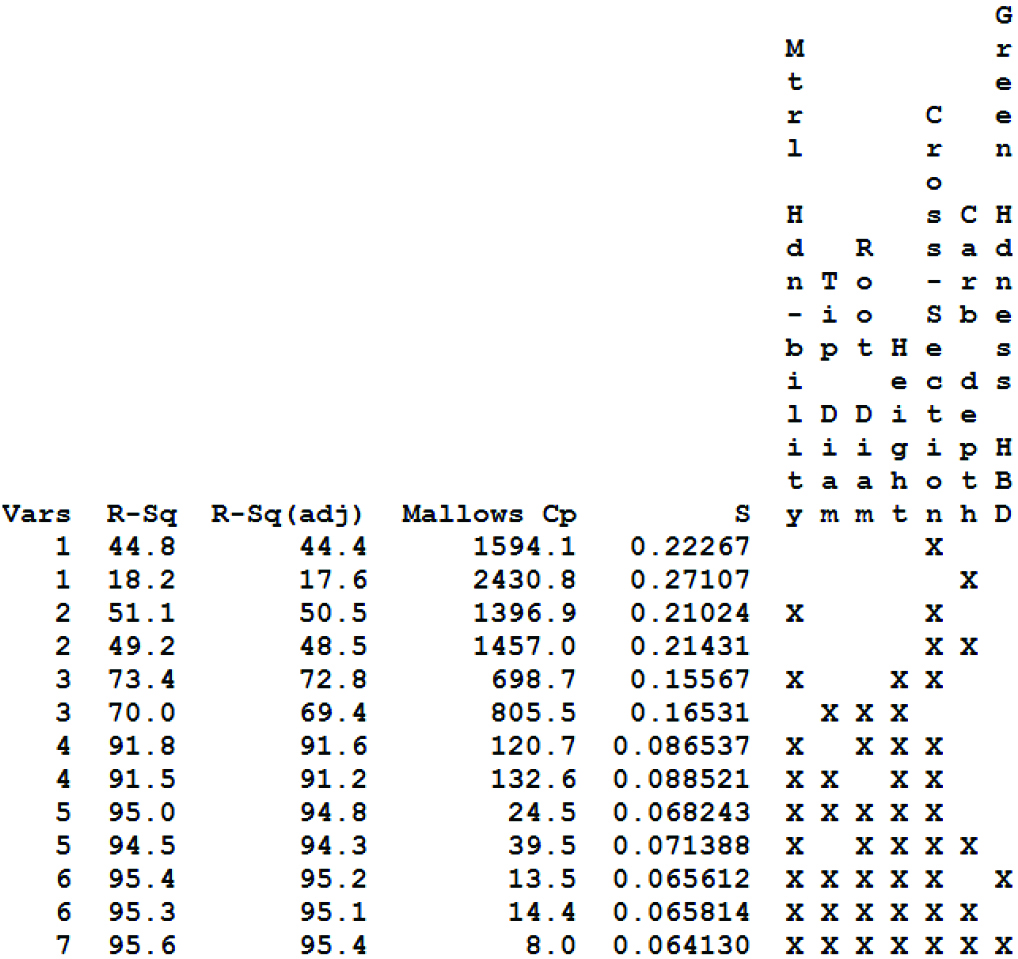
Table 4 shows the results of the ANOVA analysis on the larger dataset (19 part numbers, 314 gears) without green hardness available. The model with the selected predictors was found to be statistically significant with p-value approaching zero. OD, tip diameter, and height of the ring gear had the largest contribution to the gear MBP heat treat growth. Similar to the previous analysis, tip and root diameter were also found to be highly correlated and influencing the regression results and fitted parameters.

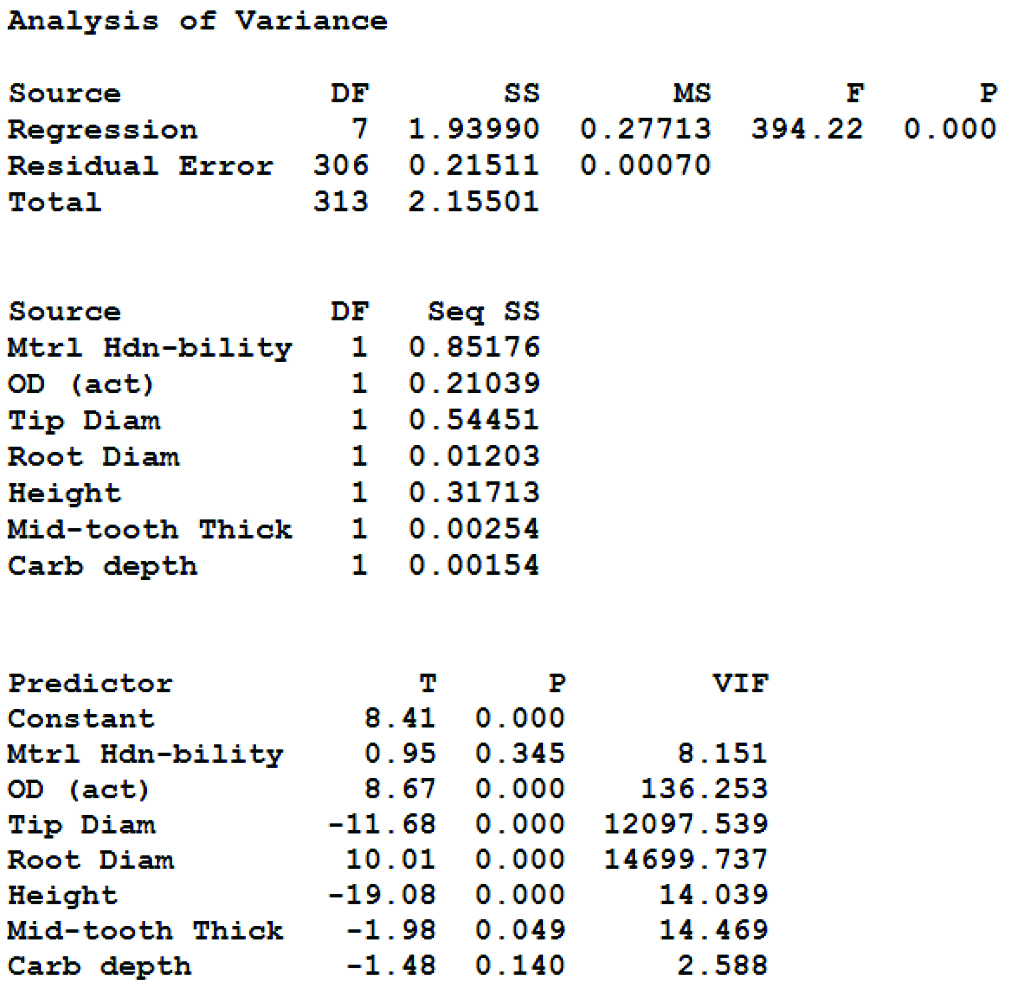
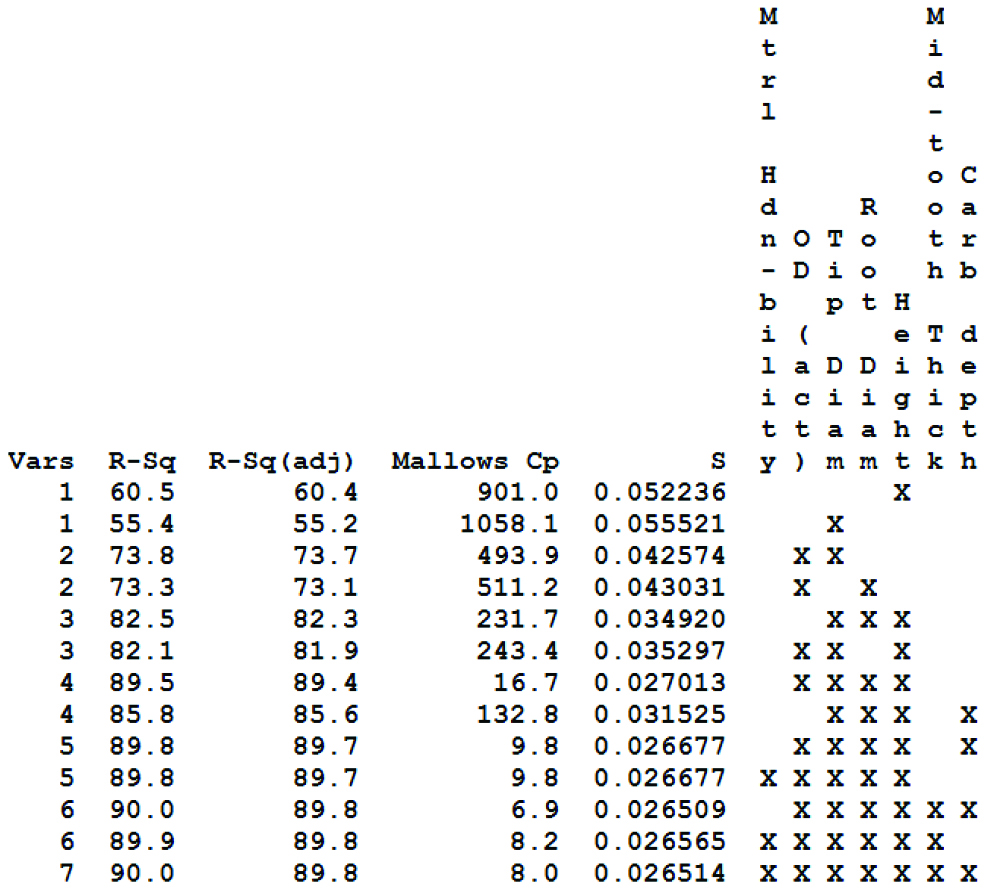
Table 5 shows the results of the best subset model analysis. As with the previous dataset analysis, gear MBP percent change revealed higher R² and greater predicting power over the actual gear MBP growth. A model with three factors — tip and root diameter and height — explained 82.3 percent of the overall observed variation but showed high Mallows’ Cp. In general, several models with five to seven factors provide 89.7-percent R²_adj with relatively low Mallows’ Cp factors. From practical considerations and the authors’ experience, material hardenability is known to be significant in influencing ring gear heat treat response. However, based on the high p-value for this factor (Table 4), the model selected as best is the one with six factors with 89.7-percent R²_adj that excludes material hardenability. The addition of future data to this analysis may provide clarity as to the effect of this factor on MBP growth.

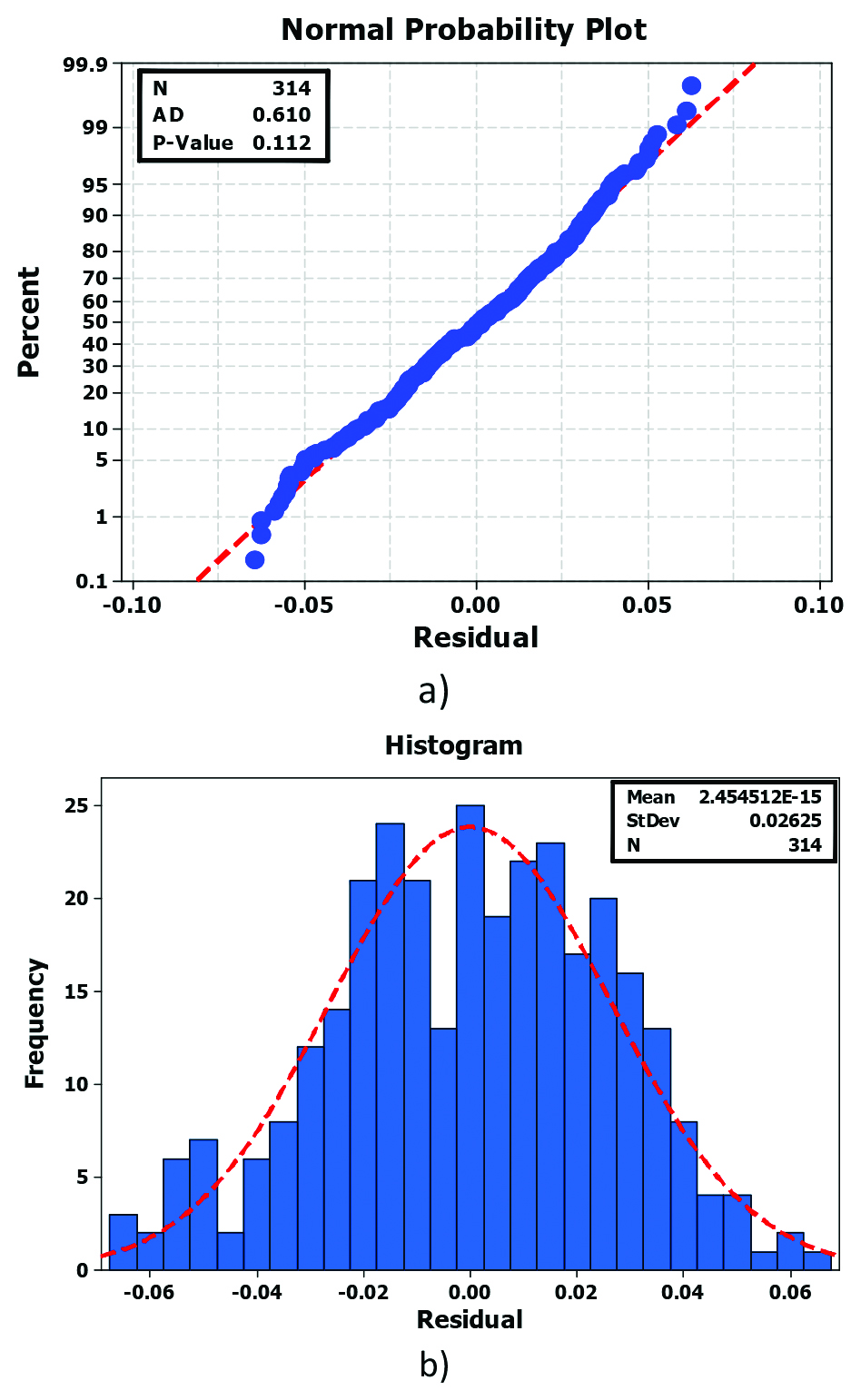
Figure 3 shows the results of the normal probability plot and residuals distribution histogram for the best subset model. Both indicate a satisfactory test for normality and confirm validity of the multiple regression analysis.

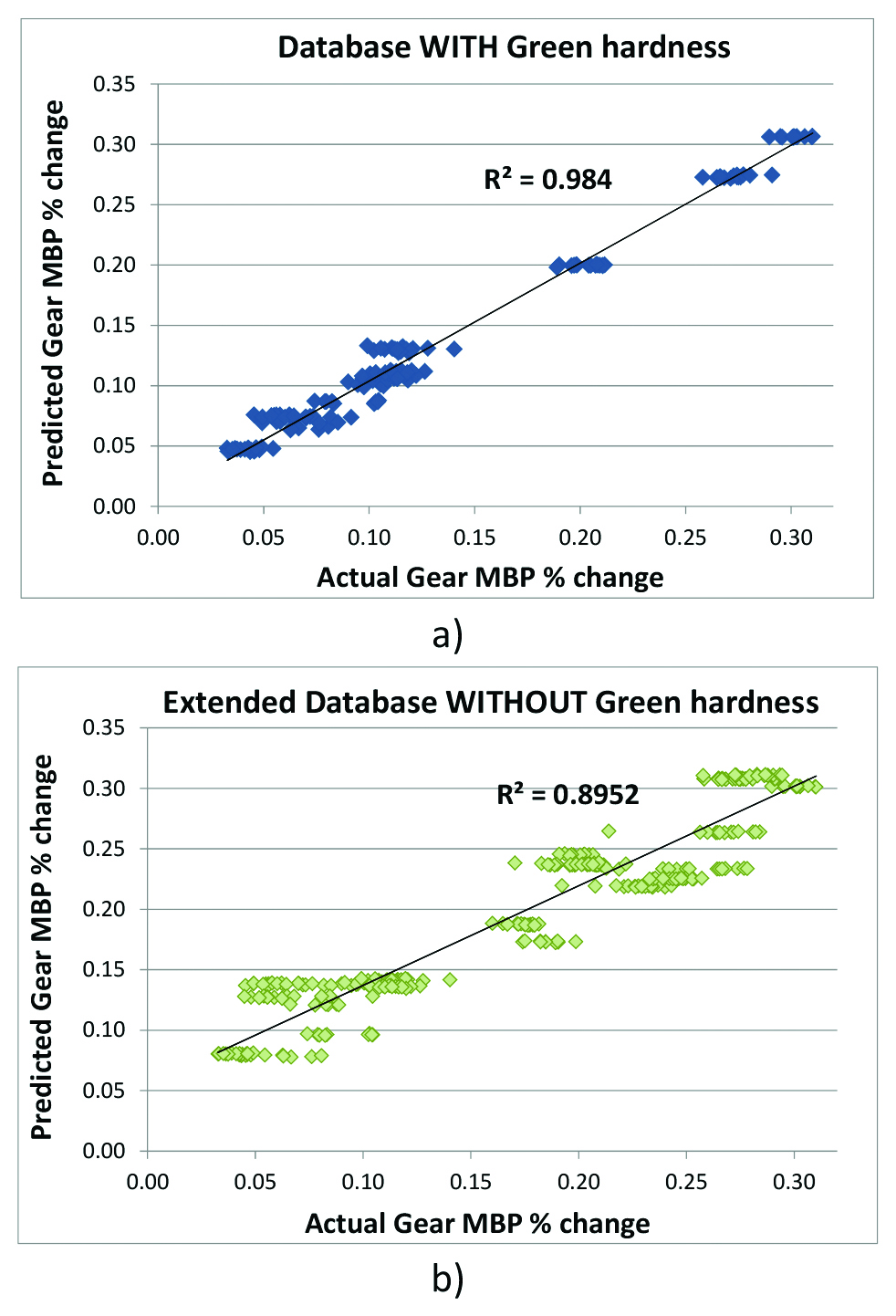
To validate the multiple regression models developed from both datasets, the regression equations were used to calculate the predicted gear MBP percent change. Figure 4 shows the predicted heat treat growth on gear MBP plotted against the experimentally observed gear MBP percent change. Note that displayed R² for the predicted versus actual gear MBP heat treat response in Figure 4 is calculated differently from the R² parameter in the multiple regression analysis (Table 2 and Table 5). The observed agreement is quite good confirming the models validity.

As mentioned previously, one hypothesis to be explored in this investigation was whether green hardness had a significant impact on the change in MBP. What can be observed in the model that includes green hardness is that it is a statistically significant factor that is not strongly adding or detracting from the model. It is important to reiterate, though, that the dataset with green hardness has relatively limited data consisting of 10 gear part numbers at the time of this paper’s publication. Further study of this factor may be warranted.

Conclusion

Ring gear HTTL database was developed to quantify and predict gear MBP growth after carburizing and hardening. Gear MBP percent change revealed greater predicting power than the gear MBP growth expressed in millimeters as it normalizes the observed heat treat growth to the actual green size of the gear. The multiple regression model developed from the smaller dataset with green hardness data revealed 98.3-percent R²_adj and utilized seven factors: material hardenability, tip and root diameter, height of the gear, cross-section, carb depth, and green hardness. The second model was developed from the larger dataset without green hardness and included a wider range of the ring gear size and geometry. The best subset model revealed 89.8-percent R²_adj and included OD, tip and root diameter, height of the gear, mid-tooth thickness, and carb depth. This is an ongoing work, as the authors continue collecting and analyzing the HTTL data and refining the model parameters. Ultimately, the use of these models is projected to reduce and possibly eliminate the need for HTTL, thus reducing gear development lead time and cost.

Acknowledgments

The authors appreciate the assistance of the Caterpillar metrology lab personnel staff in performing the CMM/PMM measurements. The authors would also like to thank Robert Hertenstein Jr., Chad Siebenaler, Md. Maniruzzaman, and Ying-Liang R. Lee for their assistance and valuable discussions.

References

1. Whitney, Daniel E. (2004). Mechanical Assemblies – Their Design, Manufacture, and Role in Product Development. Oxford University Press.
2. Davis, J.R. (2005). Gear Materials, Properties, and Manufacture. ASM International. “Fatigue and Life prediction,” p. 163-226, 293-309.
3. Dossett, Jon L. Totten, George E. (2014). ASM Handbook, Volume 4D – Heat Treating of Irons and Steels. “Selection of Carburizing Steels,” p. 68-75.
4. Michalec, G.W., Sanchez, M.I., Predicting Heat Treat Growth, American Machinist, p. 99-10, 1965.
5. Bahnsen, C., Clausen, B., Hoffmann, F., Zoch, H.-W. (2006), Influence of Carburising on Distortion Behaviour, Mat.-wiss.u.Werkstofftech, 37 (1), p. 58-62.
6. Bomas, H., Lubben, Th., Zoch, H.-W., Mayr, P. (1990), Harterei-Tech. Mitt., 45, p. 188.
7. Clausen, B., Surm, H., Hoffmann, F., Zoch, H.-W. (2009), The Influence of Carburising on Size and Shape Changes, Mat.-wiss.u.Werkstofftech, 40 (5-6), p. 414-419.
8. Kristoffersen, H., Segerberg, S. (1995), Designed Experiments to Study Distortion, Hardness and their Variations in Hot-oil-quench Carburising, Heat Treatment of Metals, 2, p. 39-42.
9. Clausen, B., Frerichs, F., Kohlhoff, T., Lubben, Th., Prinz, C., Rentsch, R., Solter, J., Surm, H., Stobener, D., Klein, D. (2009), Identification of Process Parameters Affecting Distortion of Disks for Gear Manufacture, Part II: Heating, Carburizing, Quenching, Mat.-wiss.u.Werkstofftech, 40 (5-6), p. 361-367.
10. Jurci, P., Stolar, P., Stastny, P., Podkovicak, J., Altena, H. (2008), Investigation of Distortion Behaviour of Machine Components due to Carburizing and Quenching, p. 27-3.
11. Minitab^® 17 Statistical Software Manual (2010).

Proceedings of the 28th ASM Heat Treating Society Conference. October 20–22, 2015, Detroit, Michigan. Reprinted with permission of ASM International.