The Generation-IV reactors in nuclear power plants are expected to address the growing energy demand by producing electricity and, at the same time, mitigating greenhouse gas emissions. Various reactor types, such as a Gas-Cooled Fast Reactor (GFR), Lead Cooled Reactor (LFR), Molten Salt Reactor (MSR), Sodium-Cooled Fast Reactor (SFR), Supercritical Water-Cooled Reactor (SCWR), and Very High Temperature Reactor (VHTR) are being considered.
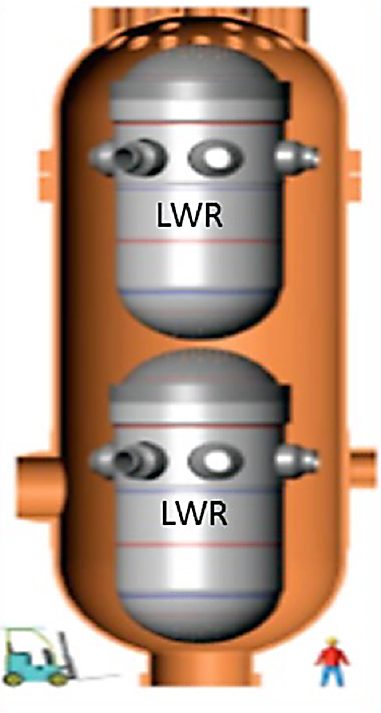
The VHTR is a Gen-IV reactor system at the heart of the so-called Next Generation Nuclear Plant (NGNP). VHTRs are designed to operate at temperatures much higher than those of currently operating reactors. Moreover, they are designed for longer service periods (60 years or more) compared to the current operating reactors [1]. Depending on the VHTR design, Prismatic Modular Reactor or Pebble Bed Modular Reactor, the operating temperature of the reactor pressure vessel (RPV) can vary between 300°C and 650°C. Furthermore, the RPV in the VHTR will be more than twice the size of a typical RPV in a Light Water Reactor (LWR) [2], as shown in Figure 1.
When a material deforms in an elastic region, the material regains its original state after the load is removed. The elastic deformation is a linear relationship in which stress is directly proportional to strain according to Hooke’s law. Materials cannot retrieve their original state when it is deformed in the plastic region. Despite the material being deformed plastically at ambient temperature, work hardening increases the strength of the material. During work hardening, prior dislocations obstruct the passage of any new dislocations, thus increasing the strength of the material. But at elevated homologous temperatures due to thermal energy, the dislocations annihilate and the work hardening is weakened. Creep deformation and rupture of metals is of great concern for prolonged service life at elevated temperatures. For an engineering structure operating in ambient temperature, creep is not considered as a significant deformation mechanism. In a high-temperature application, parameters like the duration of test, the grain size, subgrain size, precipitate size and their distribution, and effective stress all have a role in dictating the strength of a material.
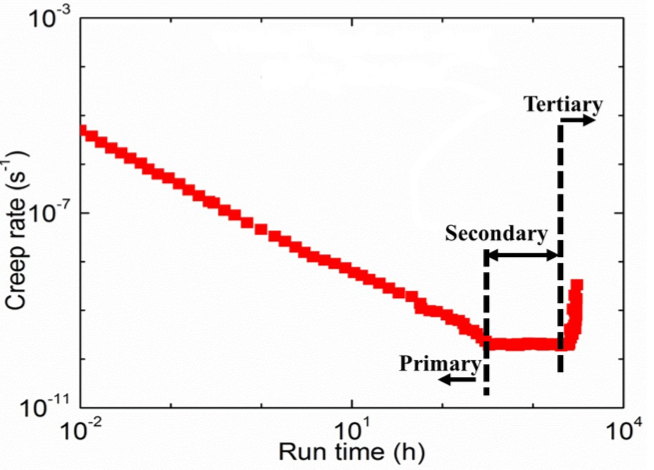
A conventional creep curve consists of three distinct stages: primary, secondary, and tertiary, as shown in Figure 2. In primary creep, the strain rate (or creep rate) decreases with time as work hardening takes the center stage. The secondary stage, also known as steady-state creep, is of vital importance as it sheds light on the creep deformation mechanism. In the secondary creep stage, the material is deformed plastically while there is a higher degree of strain hardening and increased dislocation density, resulting in a constant creep rate. Strain rate increases as time increases in tertiary creep. Increased creep rate results in necking, crack, and void formation. Tertiary creep stage is very rapid so the materials in engineering structures are designed not to enter this stage.
The operational life of a material can be predicted from the knowledge of creep deformation mechanism. Norton’s and Bird-Mukherjee-Dorn (BMD) relations are used to describe creep mechanisms. Norton’s equation is:
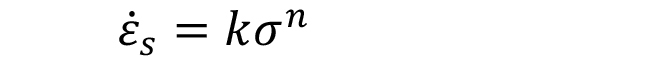where ε.s is the steady-state creep rate, σ the stress, k a constant based on material property and test condition, and n the stress exponent — a constant for a mechanism. Diffusional controlled processes dominate the high-temperature mechanical properties of metals, especially above homologous temperatures of 0.4Tm. The Bird-Mukherjee-Dorn (BMD) equation best describes the creep mechanism in this regime. BMD considers a wide range of parameters in determining the prevalent creep mechanism:
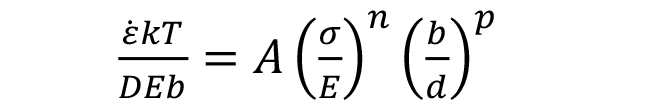where ε. is the steady state creep rate, A the microstructural mechanical constant, E the elastic modulus, b the burger vector, k the Boltzmann constant, T the absolute temperature, σ the applied stress, d the grain diameter, n the stress exponent, p the inverse grain size exponent, D the diffusivity. D is described by the following relation:
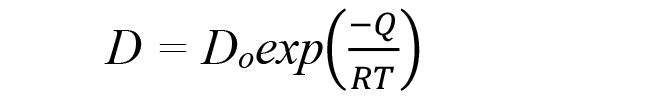where Do is the frequency factor, Q the activation energy for creep, and R the universal gas constant.
The stress exponent can be obtained by plotting creep rate (s-1) against stress (MPa). For high temperature diffusion-controlled creep, the stress exponent ranges from 1-7, which helps identify the rate-controlling creep deformation mechanism. Charit et al. [3] have identified various diffusion mechanisms and their parametric dependencies. A stress exponent of 1 is observed in Harper-Dorn, Nabarro-Herring and Coble creep also known as Newtonian viscous creep mechanisms. These are non-dislocation-based mechanisms that occur at very low stresses and high temperatures. Stress exponents of 2 and 3 are observed in superplastic materials and solute solution strengthened alloy, respectively. Dislocation climb is associated with a stress exponent of ≥5. Extremely high ‘n’ associated with high stress conditions indicates a breakdown of power-law creep. In precipitation-strengthened alloys, such as 9CrMo steels and oxide dispersion strengthened (ODS) alloys and intermetallics, such as Ni3Al, TiAl, a stress exponent above 7 has been associated with physically impossible high apparent activation energy [4,5]. Threshold stress has been incorporated to calculate effective stress, true stress exponent, true activation energy, and in identification of creep deformation mechanisms.
Creep studies carried out in 9CrMo steel at the temperature range of 600°C to 750°C and under stress of 35 to 350 MPa yielded two distinct creep deformation mechanisms. Newtonian viscous creep was observed in the low stress regime with stress exponent of n~1. The creep mechanism transitioned from the Newtonian viscous creep (n~1) to a power-law creep with high apparent stress exponents in the high stress regime. The high stress exponent was rationalized by incorporating threshold stress approach in the Bird-Mukherjee-Dorn equation, which helped identify rate-controlling mechanism as edge dislocation climb.
References
- I. Charit, K. L. Murty, Structural materials issues for the next generation fission reactors, JOM 62 (9) (2010) 67-74.
- K. L. Murty, I. Charit, Structural materials for Gen-IV reactors: challenges and opportunities, J. Nucl. Mater. 383 (2008) 189-195.
- I. Charit, K. L. Murty, J. Nucl. Mater. 374 (2008) 354-363.
- M. E. Kassner, Fundamental of Creep in Metals and Alloys, Elsevier Science, 2009.
- Shrestha, T.; Basirat, M; Charit, I.; Potirniche, G.P.; Rink, K.K. Creep deformation mechanisms in modified 9Cr-1Mo steel. J. Nucl. Mater. 2012, 423, 110–119.
