The mechanism of creep and its stages

In this column, I will discuss the mechanism of creep and its three stages.

Applications of metals at elevated temperatures involve several problems. It is known that the strength of metals decreases as the temperature increases. As temperature increases, the rate of diffusion increases. The equilibrium concentration of vacancies also increases as temperature increases. Dislocations have increased mobility at elevated temperatures through the mechanism of climb. The slip system of a metal may change as the temperature increases. The microstructural stability of the material is also of concern, as cold worked metals may recrystallize and exhibit grain coarsening. Precipitation hardening alloys, such as aluminum, may overage and lose strength as the precipitates coarsen.

Creep is the time-dependent plastic deformation of a metal or material under load. Creep usually occurs at high temperatures but can also occur at room temperature. Good examples are lead or glass. The concept of high temperature varies from material to material, as one temperature is high for one material, but not high for another material. In general, creep is considered to occur at 0.4-0.5 T_m, where T_m is the absolute melting temperature of the material (measured in °K).

When measuring the engineering creep curve of a metal, a constant axial load is applied to a tensile specimen maintained at a constant temperature. The elongation of the specimen of the specimen is measured as a function of time. The general procedures of creep testing are described in ASTM E139 [1].

The idealized shape of a creep curve is shown in Figure 1. In this curve, there are three primary stages. Primary creep where there is an initial rapid elongation of the specimen, which then decreases with time. This creep rate eventually reaches a steady state in which the creep rate changes very little with time. This is called secondary creep. In the final stage of creep, called tertiary creep, the creep rate increases rapidly until fracture occurs.

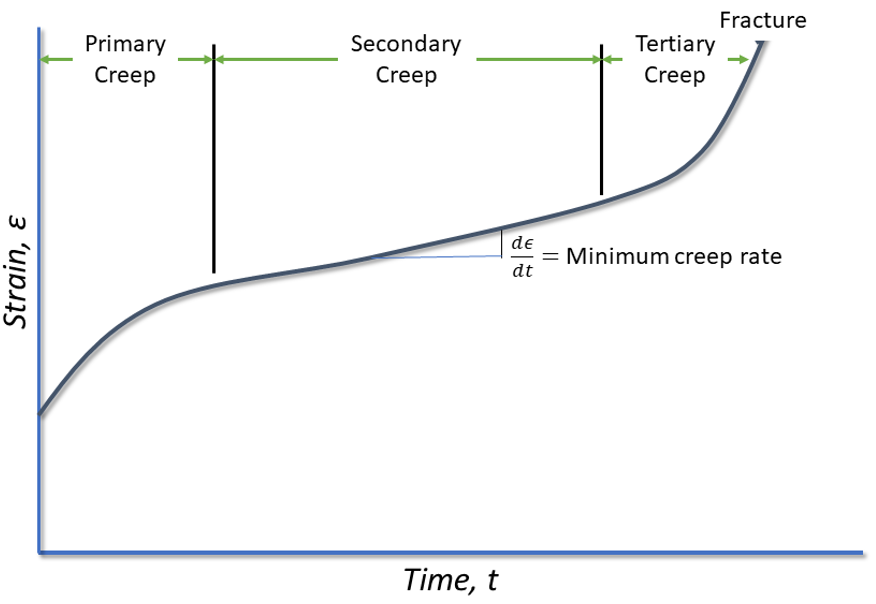
Stages of creep

The first stage of creep, called primary creep, represents a region of decreasing creep rate. This is predominantly a transient creep, where the resistance to creep by the material increases due to the deformation of the metal.

The second stage of creep, or secondary creep, is a period of nearly constant creep. This is because of the competing processes of strain hardening and recovery. This steady-state creep is called the minimum creep rate.

Tertiary creep occurs during constant-load testing at high loads and elevated temperatures. This is where there is a reduction in the cross-section of the tensile specimen because of necking (or internal void formation). This stage of creep is often associated with metallurgical changes in the metal, such as precipitation coarsening, or recrystallization.

The minimum creep rate is the most important design parameter from the creep curve. This is typically represented by the stress required to produce a creep rate of 0.001% per hour or 1% in 10,000 hours.

There has been a great deal of research into the mechanisms of creep deformation [3]. The primary dislocation mechanisms are:

• Dislocation glide.
• Dislocation creep.
• Diffusion creep.
• Grain boundary sliding.

Frequently, there will be more than one mechanism occurring at one time.

Dislocation glide involves dislocations moving along slip planes. Any barriers are overcome with thermal activation. This generally occurs at higher stress levels than would be considered for creep deformation. The creep rate is determined by the ease in which dislocations are impeded by obstacles, such as precipitates, and other dislocations.

Dislocation creep occurs by dislocation glide aided by vacancy diffusion. This is based on the idea that steady state creep is based on the competing mechanisms of strain hardening and recovery by the annihilation of dislocations.

At higher temperatures and lower stresses, diffusion creep becomes the dominant mechanism. Nabarro [4] and Herring [5] proposed that the creep process was controlled by stress-induced diffusion. They suggested that vacancies flowed from grain boundaries with tensile stresses to those that have compressive stresses, while there is a flux of atoms in the opposite direction, elongating the grain. They further suggested an equation where increasing grain size reduced the creep rate.

At lower temperatures, grain boundary diffusion dominates. This is called Coble creep [6]. In this case, Coble creep occurs through the diffusion of atoms along the grain boundary. The activation energies are different for Nabarro-Herring creep and Coble creep. From examination of the activation energies, the dominant mechanism can be determined.

Grain boundary sliding is not a significant contributor to steady-state creep, it is important for initiating intergranular fracture. Since there is mass transport from both Nabarro-Herring creep and Coble creep, voids can form at grain boundaries. Grain boundary sliding is motion of the grain boundaries to accommodate the mass transport from Nabarro-Herring and Coble creep. Voids and cavities can result at these grain boundaries (Figure 2).

Large grains slow this process, as there is less total surface area than with small grains. In a limiting case of single crystals (such as in a jet turbine blade), this mechanism is completely suppressed because there are no grain boundaries.

Precipitates can pin grain boundaries and prevent grain boundary sliding. Fine carbides, or other precipitates, can reduce grain boundary sliding. These precipitates must be small, as large precipitates can initiate voids at the interface, resulting in faster grain boundary sliding.

Conclusions

In this short article, the mechanisms of creep were briefly described. Creep is a process of applied stress at elevated temperatures greater than 40-50 percent of the absolute melting temperature, resulting in plastic deformation of the part. Large grain size reduces creep and is partially the reason that castings have preferred creep properties over wrought products of the same nominal composition.

Should you have any questions on this article, or suggestions for further articles, please contact the writer or the editor. 

References

1. ASTM, “ASTM E139-11(2018) Standard Test Methods for Conducting Creep, Creep-Rupture, and Stress-Rupture Tests of Metallic Materials,” American Society for Testing Materials, Conshohocken, PA, 2018.
2. G. E. Dieter, Mechanical Metallurgy, New York, NY: McGraw-Hill, 1976.
3. M. E. Kassner and M. T. Perez-Prado, Fundamentals of Creep in Metals and Alloys, New York: Elsevier, 2004.
4. F. R. Nabarro, Report of a Conference on Strength of Solids, London: Physical Society, 1948, p. 75.
5. C. Herring, “Diffusional Viscosity of a Polycrystalline Solid,” J. Appl. Phys., vol. 21, pp. 437-445, 1950.
6. R. L. Coble, “A Model for Boundary Diffusion Controlled Creep in Polycrystalline Materials,” J. Appl. Phys., vol. 34, pp. 1679-1682, 1963.